§ Представление чисел

Сначала, перед тем как говорить о теме, нужно знать, как представляются числа в компьютере и цифровой технике. В цифровой микроэлектронике существуют два состояния - это 0 или 1. Говорят, это называется двоичным, бинарным представлением. К примеру, за 0 можно принять минус, за 1 - плюс. Или то, выключена ли лампочка (0) или включена (1). Для наглядности, далее буду рассматривать лампочку.
Лампочка может иметь 2 состояния - либо она выключена и равна нулю (0), либо же включена и равна единице (1). Никак иначе представлять ее не будем. Например, лампочка может иметь на самом деле бесконечное количество состояний между 0 и 1, зависит от того, какое напряжение будет на нее подаваться, но поскольку это уже относится к так называемым аналоговым приборам, нас это не интересует.
Одна лампочка может нам повествовать только о числах от 0 до 1. Но что делать, если нам придется представить, например, число 3 или 4, или 100, и так далее? Поступим по аналогии. В десятичной позиционной системе счисления существуют также числа от 0 до 9 и нет других вариантов чисел. Что тогда? То есть, получается, считать на самом деле можно только от 0 до 9? А что же будет после 9? Мы уверенно скажем, что это будет 10. Однако, как можно заметить, мы использовали уже существующие цифры 1 и 0, но количество знаков (разрядов) в числе увеличилось с одного на два. То есть, если мы числа от 0 до 9 может представить одной буквой, то уже числа от 10 до 99 мы представляем двумя буквами.
Точно так же происходит с двоичным представлением. Разность заключается только в том, что в десятичной системе десять цифр, а в двоичной - два числа. Значит, что после 1 будет следовать 10 - иными словами, происходит перенос в старший разряд.
Продолжим счет. Итак:

  0 - 0
  1 - 1
 10 - 2 Попробуем добавить +1, младший разряд обнулился, в старший перенесли 1
 11 - 3 К 0 прибавился 1, стало 11
100 - 4 К 1 добавился 1, перенос в старший разряд, там 1+1 тоже дал перенос
101 - 5
110 - 6
111 - 7

Таким образом, с помощью трех лампочек можно представить 8 различных комбинаций чисел от 0 до 7. С каждым новым разрядом количество комбинации удваивается, например, 4 лампочки дадут 16 комбинации, 5 лампочек - 32 комбинации и так далее. Как нетрудно заметить количество комбинации равно , где n - количество лампочек, или разрядов, или битов. Увеличивая разрядность, можно представить какое угодно большое число.

§ Полусумматор

Полусумматор - это вычислительное устройство, которое складывает два числа, в данном случае, это будут два двоичных числа. Рассмотрим все возможные варианты сложения двух чисел a + b:

0 + 0 =  0
0 + 1 =  1
1 + 0 =  1
1 + 1 = 10 (двоичное представление 2)

Я представлю эти выражения в виде таблицы истинности:

a b | c r
0 0 | 0 0   0 + 0 = 00 (0)
0 1 | 0 1   0 + 1 = 01 (1)
1 0 | 0 1   1 + 0 = 01 (1)
1 1 | 1 0   1 + 1 = 10 (2)

Итого, как видно из таблицы, выход r = a XOR b, а выход c = a AND b. В схематическом виде это получается так

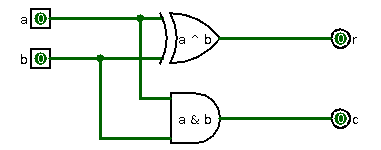
Данную схему принято называть двоичным полусумматором, или просто полусумматором. Она складывает два числа и выдает младший разряд R и перенос C.

§ Полный сумматор

Полный сумматор - это два полусумматора. Первый полусумматор складывает два числа между собой, а второй добавляет перенос из предыдущего разряда. Другими словами, двоичный полный сумматор складывает числа a + b + c. Как нетрудно догадаться, максимальным числом, при сложении полным сумматором, будет число 1+1+1=11 (десятичное 3).
Рассмотрим принцип работы полного сумматора. Необходимо сложить три числа a+b+c. Перестроим выражение так: (a+b)+c. Вначале складываем только числа a+b, и для этого у нас есть полусумматор. При сложении числа a+b получаем результат r0 и перенос c0. Теперь складываем результат r0+c и получаем результат r1 и перенос c1. В случае наличия одного из переносов, например если c0=1 или c1=1, считаем, что есть перенос в следующий разряд c=1. Если же оба переноса равны 0, то считаем, что переноса не было.
Тонкость с переносами в том, что он может быть только один. Допустим такую ситуацию. К примеру, мы получили при сложении a+b перенос c0=1. Это значит, что r0 будет равен 0 (см. таблицу истинности в полусумматоре). Итак, это так же значит, что при r0, равным 0, если сложить его с c=1 то переноса не будет, так же, как не будет переноса при c=0.
Аналогично, если есть перенос c1=1, это значит, что r0=1 и c=1. А поскольку если r0=1, это значит, что переноса c0 не было, и он всегда равен 0. Поэтому, c0 и c1 не могут быть равны единице одновременно.
Составим таблицу истинности полного сумматора:

a b c | c r  десятичные
0 0 0 | 0 0  0+0+0=0
0 0 1 | 0 1  0+0+1=1
0 1 0 | 0 1  0+1+0=1
0 1 1 | 1 0  0+1+1=2
1 0 0 | 0 1  1+0+0=1
1 0 1 | 1 0  1+0+1=2
1 1 0 | 1 0  1+1+0=2
1 1 1 | 1 1  1+1+1=3

Представим теперь это на схеме:

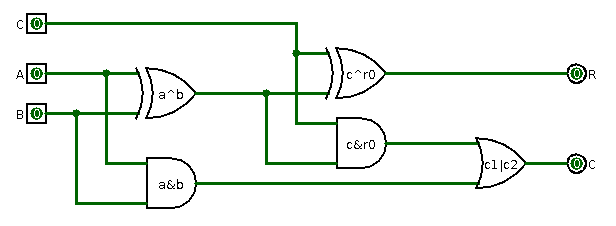
Здесь видно два полусумматора. Каждый полусумматор имеет выход переноса c0, c1, которые потом объединяются с помощью логического ИЛИ. Выход первого полусумматора идет на вход второго. В итоге получается полный сумматор, с помощью которого можно будет выстраивать схему сложения двух двоичных чисел.

§ Сложение двоичных чисел

Сложение производится в столбик, как и обычное сложение чисел, от младшего разряда к старшему. Попробуем сложить два числа 010011₂ и 001110₂:

   010011
 + 001110
---------
   100001

Рассмотрим самый правый (младший разряд):

• 1+0=1, переноса нет
• 1+1=0, запоминаем перенос
• 0+1+1 (перенос из предыдущего разряда)=0, есть перенос в старший
• 0+1+1 (перенос из предыдущего разряда)=0, есть перенос в старший
• 1+0+1 (перенос из предыдущего разряда)=0, есть перенос в старший
• 0+0+1 (перенос из предыдущего разряда)=1, переноса нет

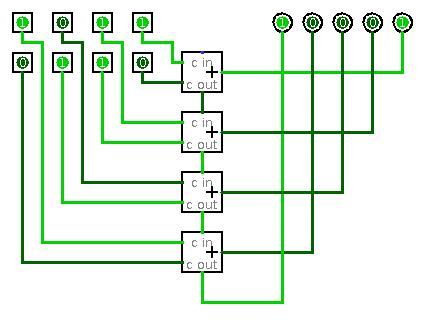
На схеме изображены четыре последовательно подключенных полных сумматора. Из предыдущего переноса каждого сумматора входит в перенос следующего разряда, тем самым получая схему сложения столбиком двоичных чисел.

§ Вычитатель

Вычитание в цифровой технике организовано, как ни парадоксально бы это ни звучало, через сложение. Все это благодаря тому, что количество складываемых разрядов ограничено и поэтому к таким операциям применяется различные правила, которые проистекают из правил сложения по модулю.
Что такое сложение по модулю? И вообще что такое модуль? Модуль - это остаток от деления на число. К примеру, число 7 по модулю 3 будет 1. Почему? Если мы поделим число 7 на 3, то получим целое число 2, и остаток 1. Проверим:

• 7-3=4
• 7-3=1

Остаток 1, всего вычитаний было 2. Значит, 7 делить на 3 равно целое число 2, и остаток 1. Целое число при вычислении по модулю, отбрасывается и получается только 1:
Если число в двоичном представлении представлено в 4 разрядах, то как мы помним, в 4 разряда можно поместить только числа от 0 до 15. После того как мы прибавим 15+1, получится не 16, а 0 - то есть, получается, что любое 4-разрядное двоичное число это модуль по 16. Следовательно, 17 это будет 1, 33 тоже будет 1 и так далее. Число будет словно вращаться по кругу.
Существует следующая простая формула
Теперь попробуем представить число -1 в 4-х разрядной системе:
Ясное дело, что 16 по модулю 16 всегда будет давать 0, поскольку любое число, которое делится само на себя, никогда не может дать остатка. Также не дает остатка любое число, которое делится на кратное себе число, иными словами .
Получается, чтобы получить отрицательное число, его можно выразить через положительное через сложение с , где n-это количество разрядов в хранимом в компьютере числе. А это количество, даже если оно очень большое, всегда ограничено, поскольку компьютер не может запомнить бесконечное количество информации.
Таким образом, получается что:

• -1 = 15
• -2 = 14
• -8 = 8

Однако, тут возникают всякие интересные свойства с так называемым "дополненным кодом", что в принципе то можно сказать, что число 7 это тоже самое что -9, однако, начнутся ошибки, которые будут связаны с переносом в самый старший разряд. Поэтому говорят, что число тогда и только тогда отрицательное, когда старший разряд числа равен 1, и наоборот, если он равен 0, то такое число является положительным.
Есть удобный алгоритм для перевода отрицательных чисел в двоичное представление. Допустим, что у нас 4-х разрядное число. Оно по определению явно не может вместить в себя число 16, поэтому мы делаем так:

• Вычитаем из 16 единицу, получаем 15
• Число 15 представляет из себя все установленные биты (1111)
• Вычитаем из 1111 необходимое нам число, к примеру 10 (2)
• Получаем 1101 (15-2=13)
• Прибавляем единицу обратно (13+1=14), тем самым восстанавливая справедливость

Математически это будет выглядеть так
Формула кажется невероятно сложной, но на самом деле все очень и очень просто получается.
Дело в том, что дает все единицы в числе n-ой разрядности. Например если мы возьмем n=3, то будет число 111 (7), если n=5, то число 11111 (31) и так далее.
Из этого числа и производится процедура вычитания. Однако, и сама процедура вычитания крайне проста и не требует даже не то что переносов, не требует даже сложных каких-то элементов. Допустим, мы из 1111 вычитаем число 1001. Есть только два возможных случая: если из 1 вычесть 0, то получится 1. Если из 1 вычесть 1, то получится 0. То есть это просто инвертирование битов!
Получается, что если вычесть из 1111 число 1001, мы гарантированно получаем 0110:

  1111
- 1001
-------
  0110

Здесь все просто и элементарно. Добавить единицу не составляет сложности - для этого необходимо воспользоваться входящим переносом в полный сумматор на самом младшем разряде.

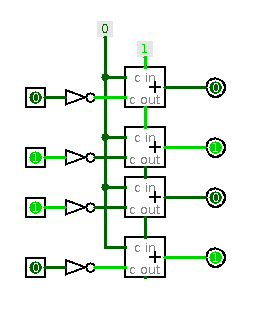
На схеме выше показан элемент преобразования числа 0110 (6) в число 1010 (эквивалент -6). Второй операнд подсоединен к 0, но сюда можно подсоединить другое число для сложения.
Теперь самое главное. Как же складываются эти числа? Представим, что надо сложить -2 и 5:
Как мы помним, -2 это 14. Потом 14 складывается с 5 и получается число 3. То есть, представляя числа в дополненном коде через операцию NEG, описанную выше, можно просто складывать два числа, и получать вычитание! Все элементарно. Но чтобы получить вычитание, нужно обязательно привести входящий операнд к необходимому виду.