Рассмотрим иллюстрацию, где зеленым закрашен параллелограмм, заданный двумя векторами и . Задача в том, чтобы рассчитать его площадь.

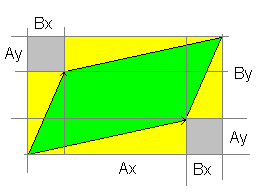
Зеленой областью выделен сам параллелограмм, желтой и серой - области, находящиеся вне его, но внутри прямоугольника, образованного путем умножения .
Расчет площади параллелограмма здесь достаточно прост, для начала надо вычислить общую площадь всего прямоугольника, в который входит этот параллелограмм, а потом вычесть желтые и серые области.
На картинке ясно видно, что общая площадь серых треугольников равна (поскольку их два). Теперь обратим внимание на то, что существуют четыре прямоугольных треугольника со сторонами Ax и Ay, а также Bx и By. Площади прямоугольных треугольников равны:
Однако, поскольку их по двое, то получается, что общая площадь всех закрашенных желтым цветом прямоугольных треугольников равна:
Теперь мы знаем все площади, которые окружают параллелепипед, пришло время найти его сам. Сам же он будет равен тому, что останется после вычитания из площади прямоугольника, в который он вписан, минус площади областей, которые только что были найдены:
Как можно заметить, полученное выражение является определителем матрицы