§ Трехмерные координаты
В предыдущей статье я подробно рассказал о том, как найти текстурные координаты на ортогональной проекции в двухмерном пространстве. Сегодня я расскажу о том, как найти их, но уже в трехмерном пространстве. По всей видимости, это работает только для трехмерного измерения, поскольку для каждого пространства необходимы собственные подходы и вычисления, хотя суть всегда остается той же самой.Для начала, надо рассмотреть следующую иллюстрацию
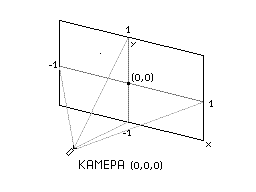
Здесь показано положение точки камеры в пространстве, а также то, как она смотрит в это пространство. Точка камеры всегда будет в положении для удобства, но и не только, ибо это не нужно для проекции, все необходимые преобразования, такие как поворот, изменение размера, перенос, будут проходить другим способом. Для алгоритма, находящего точки пересечения на треугольнике, нет необходимости выполнять такие преобразования.
Итак, камера смотрит на некую плоскость, которую еще можно называть проецирующей плоскостью, и расстояние до этой плоскости пусть будет равным dz. В данном случае dz = 1 для удобства, хотя можно взять и другие значения, но сейчас это не имеет смысла. Также можно обратить внимание на то, что есть dx и dy, которые принимают значения от -1 до 1 каждый. Для dx = -1 это значит, что проецирующий луч проходит по левому краю плоскости проекции, для dx = 1 - по правому, точно также как dy = -1 по низу, а dy = 1 по верху. Это тоже не является жестко заданным условием, но вместе с тем, сейчас это все только для удобства.
Это - виртуальный экран, на который будет отображаться треугольник (или другие фигуры, если требуется). Треугольник же задается в пространстве с помощью векторов , и точки , которая будет опорной точкой для этих векторов. На самом же деле, это задается не треугольник, а плоскость, но поскольку треугольник лежит на плоскости, то можно сказать, что и треугольник.
Задача в том, чтобы найти точку пересечения луча, идущего от камеры сквозь проецирующую плоскость (или виртуальный/реальный экран) с плоскостью (и треугольником, на ней лежащим). Для этого надо также параметрически задать уравнение луча. Ясное дело, что вектор луча , где точка это точка на поверхности проецирующей плоскости.
§ Решение задачи пересечения луча и плоскости
Имеем два параметрически заданных уравнения для плоскости и луча:Я опустил во втором уравнении стартовую точку, поскольку там она равна 0, как и условились ранее. Поскольку по условию задачи точка это точка пересечения луча и плоскости, то это значит, что два уравнения нужно приравнять, чтобы получить его решение:
И по итогу, раскладывая на координаты мы получим следующую систему уравнений:
Я заменю на , чтобы упростить чтение уравнения, а также перенесу неизвестные в левую часть уравнения:
Что по итогу наблюдается? Обычная система линейных уравнений с тремя неизвестными. В данном случае это как раз текстурные позиции на плоскости, заданной параметрически (собственно, это и есть параметры), а также - расстояние до плоскости, которое может служить мерой дальности до найденной точки, но это можно считать и по-другому, с помощью как раз тех самых найденных параметров. Зная параметры, можно рассчитать также и точное местоположение не только точки текстуры, но еще и самой точки, что бывает также очень важно при растеризации и создания, к примеру, шейдерных программ.
§ Вычисление
Чтобы решить СЛАУ, можно воспользоваться разными методами, но здесь лучше всего подойдет именно метод Крамера, который очень распространен для такого рода решения. К тому же любой другой метод будет сложнее для понимания, вычисления, и приведет к тому же самому результату.Надо найти определить матрицы по методу нахождения определителей (см. Википедию).
Замечу, что dz тут будет константой и вообще по условию dz = 1.
По методу Крамера, чтобы вычислить потребуется найти еще 3 определителя
Все очень просто! Теперь остается лишь только начать вычислять. Для оптимизации расчетов можно сказать следующее: меняются только dx, dy, все же остальные константы можно вычислять один раз для треугольника. Так работают видеокарты, которые не считают все подряд, а перед рендерингом высчитывают константы и работают только с ними.
Замечу еще кое-что. Чтобы рассчитать на поверхности плоскости, который пересек луч, необходимо домножить на , поскольку здесь выступает лишь как множитель для . Расчет параметра годится для задач по рейтрейсингу, для установления ближайшей точки пересечения с плоскостью.
§ Программная реализация
Сейчас я приведу программный код, который будет являться справочным материалом.1// Сначала, получаем разности 2float ABx = b.x - a.x, ACx = c.x - a.x, 3 ABy = b.y - a.y, ACy = c.y - a.y, 4 ABz = b.z - a.z, ACz = c.z - a.z; 5 6// Рассчитываем коэффициенты 7float A1 = (a.y*ACz - a.z*ACy), 8 A2 = (a.z*ACx - a.x*ACz), 9 A3 = (a.x*ACy - a.y*ACx), 10 // --- 11 B1 = (a.z*ABy - a.y*ABz), 12 B2 = (a.x*ABz - a.z*ABx), 13 B3 = (a.y*ABx - a.x*ABy), 14 // --- 15 C1 = (ABz*ACy - ABy*ACz), 16 C2 = (ABx*ACz - ABz*ACx), 17 C3 = (ABy*ACx - ABx*ACy), 18 // --- 19 D1 = (ACy*ABz - ABy*ACz), 20 D2 = (ABx*ACz - ACx*ABz), 21 D3 = (ACx*ABy - ABx*ACy); 22 23float u = dx*A1 + dy*A2 + dz*A3; 24float v = dx*B1 + dy*B2 + dz*B3; 25float D = dx*C1 + dy*C2 + dz*C3; 26float t = a.x*D1 + a.y*D2 + a.z*D3; 27 28if (D != 0) { 29 30 u /= D; 31 v /= D; 32 t /= D; 33 x = t*dx; 34 y = t*dy; 35 z = t*dz; 36 37} else { 38 u = v = t = 0; 39}
§ Уравнение плоскости
Из полученного уравнения есть важный вывод, это уравнение плоскости:D1*x + D2*y + D3*z + t = 0Поэтому, из этих данных легко получить нормаль (D1, D2, D3). Возможно, плоскость повернута с другой стороны (левосторонняя или правосторонняя).
Также есть старый материал по этой теме.
§ QBasic 4.5
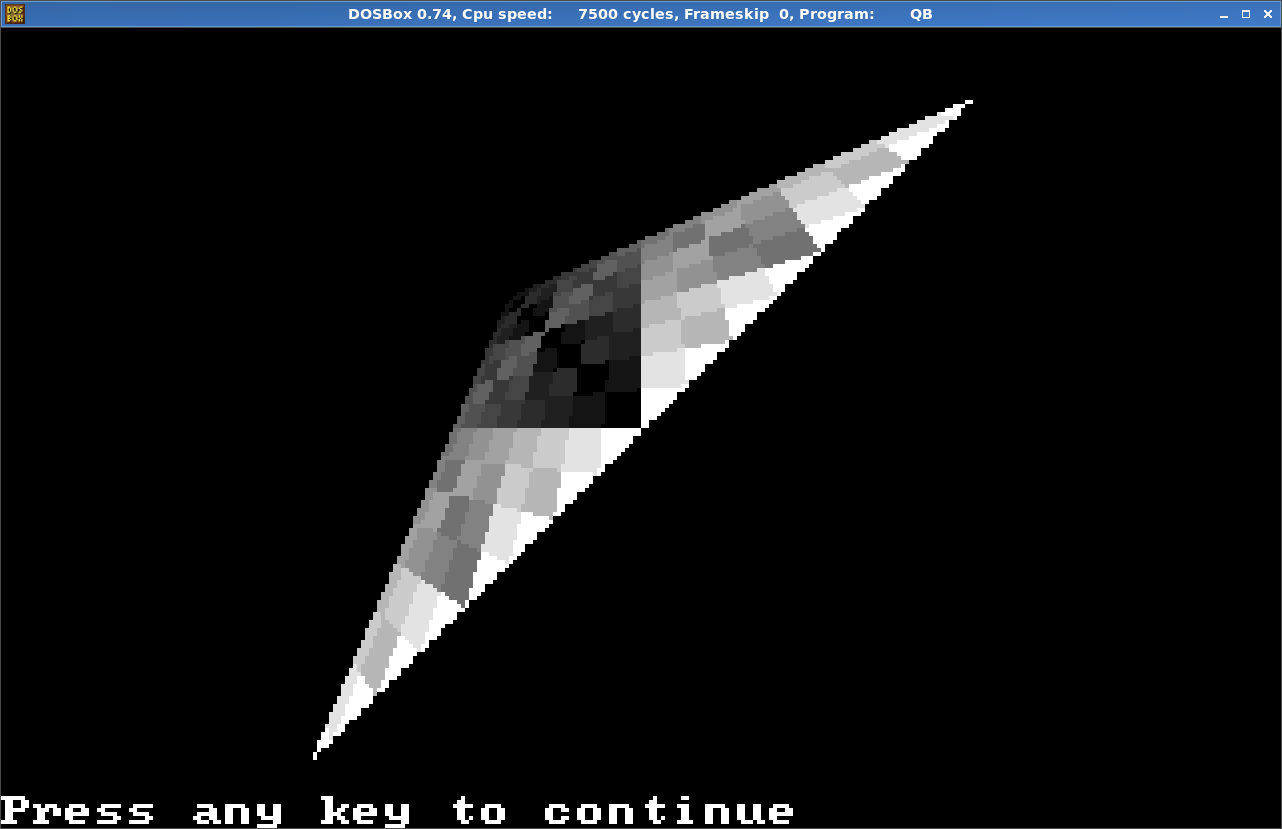
Пример реализации на языке программирования BASIC1SCREEN 13 2 3' Координаты треугольника 4Ax = -5: Ay = 5: Az = 15 5Bx = 5: By = 5: Bz = 6 6Cx = -5: Cy = -5: Cz = 6 7 8' Предварительный расчет 9ABx = Bx - Ax: ACx = Cx - Ax 10ABy = By - Ay: ACy = Cy - Ay 11ABz = Bz - Az: ACz = Cz - Az 12 13A1 = ( Ay * ACz - Az * ACy): A2 = ( Az * ACx - Ax * ACz): A3 = ( Ax * ACy - Ay * ACx) 14B1 = ( Az * ABy - Ay * ABz): B2 = ( Ax * ABz - Az * ABx): B3 = ( Ay * ABx - Ax * ABy) 15C1 = (ABz * ACy - ABy * ACz): C2 = (ABx * ACz - ABz * ACx): C3 = (ABy * ACx - ABx * ACy) 16 17' Растеризация 18FOR y = 0 TO 200 19FOR x = 0 TO 320 20 21 ' Проекционный луч 22 dx = x - 160 23 dy = 100 - y 24 dz = 100 25 26 ' Расчет координат 27 u = dx*A1 + dy*A2 + dz*A3 28 v = dx*B1 + dy*B2 + dz*B3 29 D = dx*C1 + dy*C2 + dz*C3 30 31 ' Плоскость не должна быть параллельна лучу проекции 32 IF D <> 0 THEN 33 34 u = u / D 35 v = v / D 36 c = (15 * u XOR 15 * v) + 16 37 IF u >= 0 AND v >= 0 AND u + v <= 1 THEN PSET (x, y), c 38 39 END IF 40 41NEXT 42NEXTЧто в итоге получается
