§ О целых числах

Иногда мне кажется, что это самый страшный для понимания флаг, когда-либо существовавший в целом. Его очень сложно понять и получить. Для начала, разберемся, что такое переполнение?
Дело в том, что целые числа представлены в компьютере в "дополненном коде", когда старший бит некоторого регистра равен 0 или 1. Если старший бит равен 0, то такое число считается положительным (равно или больше 0), и если старший бит равен 1, то такое число представлено как отрицательное (меньше 0). Также, числа всегда ограничены некоторым количество бит, например 8 бит, 16, 32, 64, и так далее.
Пример 8 битных чисел:

01111111 -- 127  Старший бит 0 (положительное)
11111111 -- -1   Старший бит 1 (отрицательное)
10000000 -- -128
00000011 -- 3

§ О переполнении

А что такое переполнение? Это то, когда, складывая или вычитая числа, получаем число не того знака, которое надо было бы получить. Какой можно привести пример? Очень простой!
Как можно увидеть, число минус 128 (-128) представлено в виде 10000000₂. Если сложить -128 + (-128), то, по законам математики, должно быть -256. А если сложить число 10000000₂ + 10000000₂ то получится 0! (с переносом в старший разряд). А что такое 0? Это число положительное! Ясно дело, что положительное.
Что же получается? Складываем два минуса, должен получиться минус, а получается плюс! Ошибка переполнения. Поэтому, когда процессор складывает и вычитает числа, он после каждой такой операции говорит, переполнен ли результат или нет. А как он говорит? Он обычно ставит флаг, например V или O, в котором:

• Если результат переполнен, то ставится V=1
• Если нет, то ставится V=0

§ Переполнение при сложении

А теперь, рассмотрим все возможные случаи, когда может или не может быть переполнение при сложении. Сначала скажем так, есть два операнда (A, B) и результат (C). При этом рассматривается только знак! Сами по себе значения там не играют роли.

A B C | V
+ + + | 0, плюс  на плюс  дает плюс   (+2+2=+4)
+ + - | 1, плюс  на плюс  дает минус! ---------
+ - + | 0, плюс  на минус дает плюс   (+4-2=+2)
+ - - | 0, плюс  на минус дает минус  (+2-4=-2)
- + + | 0, минус на плюс  дает плюс   (-2+4=+2)
- + - | 0, минус на плюс  дает минус  (-3+1=-2)
- - + | 1, минус на минус дает плюс!  ---------
- - - | 0, минус на минус дает минус  (-4-2=-6)

Как можно заметить, переполнение случается только в двух лишь случаях, когда плюс на плюс дает минус и когда минус на минус дает плюс. И всё! Больше случаев не бывает.
Теперь задача — как сделать так, чтобы уместить это в логическую формулу?
На самом деле, очень просто:

• Сначала надо отсеять те, у которых разный знак A и B
• Потом отсеять те, у которых одинаковый знак A и C

То есть, другими словами:

1if ( (A == B) && A != C) V = 1;
2if (!(A != B) && A != C) V = 1;

Или, если перевести на логическую схему, это будет выглядеть так:

V = (A xor B xor 1) & (A xor C)

Здесь xor 1 выполняет роль NOT.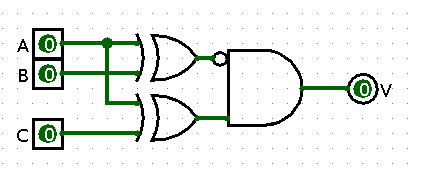

§ Переполнение при вычитании

При вычитании переполнение выполняется аналогичным образом. Поскольку вычитание - это отрицание знака, то тогда плюс меняется на минус, а минус на плюс. Как и ранее, составлю такую же таблицу, но для вычитания

A B C | V
+ + + | 0, (+4)-(+2)=(+2)
+ + - | 0, (+1)-(+2)=(-1)
+ - + | 0, (+1)-(-2)=(+3)
+ - - | 1, (+a)-(-b) больше 0 всегда
- + + | 1, (-a)-(+b) меньше 0 всегда
- + - | 0, (-3)-(+4)=(-7)
- - + | 0, (-4)-(-6)=(+2)
- - - | 0, (-3)-(-1)=-2

Итак, ситуация здесь другая. Есть только 2 случая, когда происходит переполнение. Первый случай это когда из положительного числа вычитается отрицательное и получается отрицательное. Такого не может быть, потому что: a-(-b)=a+b. Поскольку a,b - положительные числа, то и результат тоже будет положительным. Также, если из отрицательного числа вычитается положительное, то положительным результат тоже никак не может быть, потому что -a-b всегда меньше 0.

• Оставляем сначала те случаи, когда A не равно B
• И те, когда A не равно C

1if (A != B && A != C) V = 1;

Логическая функция этого выражения выглядит так:

V = (A ^ B) & (A ^ C)

Единственным отличием от предыдущего выражения это то, что убирается отрицание NOT перед A и B. Не буду приводить схему на логисиме, она и так выше нарисована, просто надо убрать отрицание на входе логического вентиля "И".