§ Деление столбиком

Все знают со школьной скамьи, как делить столбиком. Сегодня я буду делить именно столбиком, но в двоичной системе счисления. Как это сделать, разберемся получше. Допустим, надо разделить число 1101 (13) на 0011 (3). Как можно сделать. Я делаю так. Есть две части - левая часть (R), где будут проходить вычисления и правая часть, где будет находится делимое (A):

R      A
0000 | 1101
0011 <- B

Делитель B находится под операционной частью R. Для того, чтобы получить результат, необходимо сделать ровно 4 шага.
Шаг 1.
Сдвигаем влево значение A и R, задвигается старший бит из A в младший бит R. В младший бит A задвигается 0 (или вообще что угодно, например, следующее делимое).

0001 | 1010
0011 | 0 <-- здесь будет ответ

Как видим, если R < B (а он меньше, так как 1 меньше 3), то пишется в старший бит ответа число 0.
Шаг 2.
Выполняем ту же самую процедуру. Сдвигаются A,R на 1 бит влево:

0011 | 0100
0011 | 01??

Теперь же, 11 сверху равно или больше чем 11 снизу, так что вычитаем и добавляется в ответ бит 1, это будет уже 3-й бит результата.
Однако, раз вычитание было произведено, то тогда вычитается значение 11-11 и пишется в R результат 0000.
Шаг 3.
С учетом того, что теперь в R=0000, вдвигая еще один бит, получаем что там опять будет 0000:

0000 | 1000
0011 | 010?

Видно, что 0000 явно меньше чем 0011, так что пишем в бит 2 ответа результат 0.
Шаг 4.
Последняя итерация. Вдвигаем еще один, последний бит:

0001 | 0000
0011 | 0100

Соответственно, 1 меньше чем 11, так что в 1-й бит результата уходит число 0.
Деление закончено! Что по итогу имеется.

• Деление 1101 на 0011 дало отчет 100 (13 делить на 3 равно 4)
• Остаток от деления находится в R, и там 1.

Все верно!

§ Одна стадия вычитания на Logisim

Теперь я сделаю ровно то же самое, что делал сейчас, но использую для этого программу Logisim.
Для начала, необходимо сделать лишь одну стадию, один шаг. Как он работает:

• Есть вход A (делимое) и вход R (остаток), а также вход B (делитель)
• Сдвинуть A, R влево на 1 бит
• Если R >= B, вычесть R и на выход R' = R - B (результат 1) и если R < B, то на выход результат 0, R' = R
• Соответственно, на выходе A' = A << 1

Вот такая вот логика работы одной стадии.

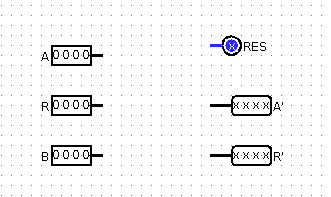
Рис 1. Так выглядят пины входа и выхода
Это лишь пины, теперь же надо сделать сдвиг влево на 1. В схемотехнике любой сдвиг — это просто вопрос переставления проводов. Не требуется вообще ничего, кроме как переставить провода:

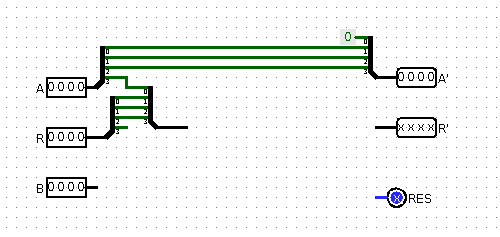
Рис 2. Перестановка проводов
На исходящих пинах A' теперь сдвинутое значение влево, в том числе в младший бит задвигается 0.
Теперь же — самое главное, это вычитание R - B, и дальнейшее сравнение что из этого получается.

Рис 3. Вычитание и компаратор
В данном случае, вычитается из нового значения R (текущий остаток) делитель B. Если получается, что R < B, то в таком случае перенос будет равен 1. Но для ответа это неправильное значение, потому что если R < B, то надо считать, что ответ 0, и наоборот, если R >= B, то ответ 1, потому на выходе поставлен инвертор (логическое НЕ).
Теперь осталось решить последний, насущный вопрос. Если ответ будет 0 (именно ответ), то в таком случае, надо выбрать то значение R, которое было после сдвига на 1 влево, или, если ответ будет 1, то тогда выбрать результат вычитания. И тут на помощь приходит мултиплексор.

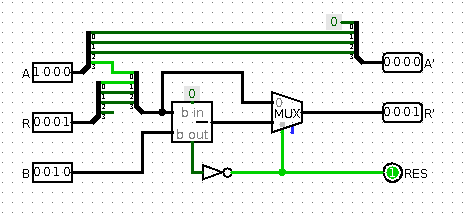
Рис 4. Добавление мультиплексора
В данном случае мы видим, что ответ 1, и мультиплексор выбирает результат вычитания. В другом случае, при ответе 0, результат бы выбирался тот, который был до вычитания R.
Это лишь одна стадия. Теперь же можно сделать тремя способами:

• Подключение всех стадии без тактов — работает настолько быстро, насколько получится, требует много логики
• Вычисление последовательно — то есть после подачи 4 тактов, мы будем получать ответ через каждые 4 такта — работает медленно, задержка в N тактов
• Вычисление в конвейере — много логики, регистров, быстро (1 результат за 1 такт), но требует предварительной загрузки конвейера

§ Деление без тактов

Сначала рассмотрю самый простой вариант деления, это просто подключить все 4 стадии одну за другой.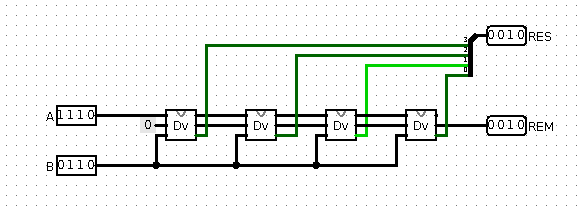

Рис 5. Подключение через последовательность
На рисунке обозначены 4 блока. Вход сверху слева — это делимое (A), далее идет 0 - текущий остаток на начало, он всегда будет 0, далее идет делитель B.
После получения старшего бита результата, на выходе A' оказывается сдвинутый на 1 предыдущий A, в R - остаток от одной стадии деления. Так повторяется 4 раза, получая полный результат. Тут все очевидно и не требуется отдельных пояснений.

§ Деление последовательно через такты

Эта схема уже будет посложнее, но она на самом деле, тратит меньше логики, потому что здесь требуются лишь регистры нужной разрядности и один блок вычитания, и один мультиплексор. То есть, эту схему легко масштабировать до любого количества битов, все зависит лишь только от наличия необходимых регистров.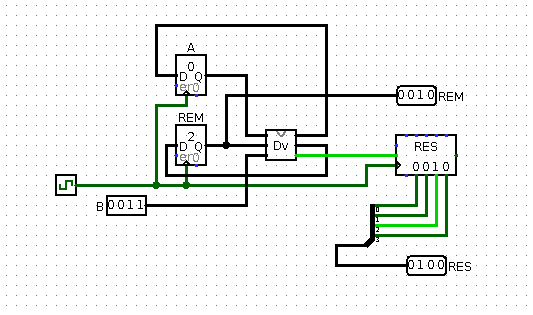

Рис 6. Последовательное деление 14 на 3
На вход регистров A и REM поступают выходные данные из стадии делителя, а на выход сдвигового регистра поступают результаты. Старший бит результата оказывается тут, правда, справа, потому я поставил там разветвитель и выровнял биты так, чтобы результат был точным.
Ядро делителя остается прежним, но все это дело тактируется через тактовый генератор извне, промежуточные результаты записываются в регистры. Чтобы получить результат, необходимо 4 раза выполнить тактирование. В регистре A будет 0, в регистре REM будет остаток и в сдвиговом регистре будет RES, результат.

§ Конвейерное деление

Деление через конвейер объединяет в себя два вышеназванных варианта. Во-первых, все стадии раскладываются, а во-вторых, для каждой стадии используется промежуточный регистр.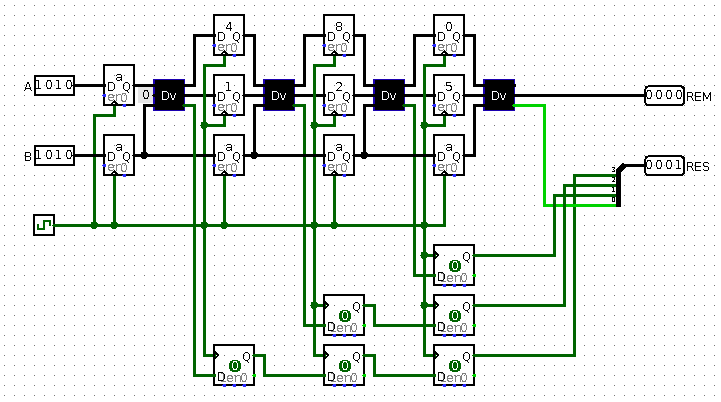

Рис 7. Четырехстадийный конвеер для делителя
Что дает конвейер? У него есть некоторые преимущества, но недостатков тоже хватает.

• Плюс. Скорость вычисления быстрая потому что по своей сути, выполняется раз 1 такт только 1 стадия
• Минус. Требуется очень много регистров и логики
• Минус. Требуется загрузка конвейера. Получается, что придется ждать 4 такта до того, как будет получен результат
• Плюс. При массовом делении, каждое новое деление получается за 1 такт, а не за 4

То есть, если нам требуется разделить число один раз, то конвейер использовать можно, поскольку ждать придется примерно столько же, сколько и последовательное деление. Но если требуется поделить 8 чисел, то выгода от использования очевидна. Деление обычным методом будет выполнено за 4 x 8 = 32 такта, а деление конвейером за 4 (предзагрузка и первое деление) + 7 (исполнение оставшихся 7 делений) = 12 тактов, то есть, аж в 2 раза. При массовости (где n - количество чисел для обработки), коэффициент будет все возрастать до количества, равного количеству битов:
Принцип работы конвейера очень прост - между исполнительными блоками установлены регистры, которые фиксируют предыдущее значение. При получении на них позитивного фронта, они защелкиваются, передавая на следующий этап новые значения. Тем самым образом, в конвейере записываются все стадии и потому туда можно после каждого защелкивания подавать новое значение.
Небольшая сложность есть в хранений результата. Результат первой стадии передается на регистр второй стадии, тот на третий и третий уже на выход, тем самым обеспечивая передачу и сохранение данных результата.
Файл логисим для скачивания также оставляю тут.

§ Модификация стадии

На самом деле, можно было бы решить вопрос более просто, задвигая в одной стадии деления не 0, а результат. Через 4 сдвига получится готовый результат. Для этого поправлю провод на выходе: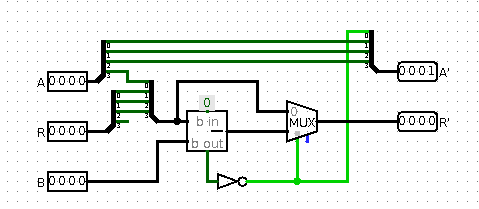

Рис 8. Результат идет на следующий вход A
Поэтому теперь все гораздо проще.

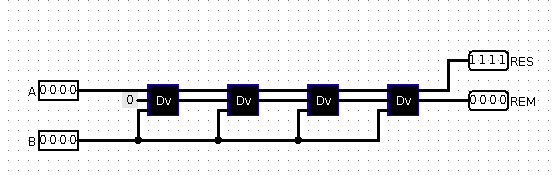
Рис 9. Проброс результата через сдвиги выхода A
Обращу внимание на один любопытный факт. В таких схемах деление на ноль дает всегда максимальный результат. Алгоритм реализует "бесконечность" таким вот способом, выдавая максимально возможный результат. Это обусловлено тем, что меньше нуля ничего не может быть в двоичном коде, поэтому результат всегда будет 1.

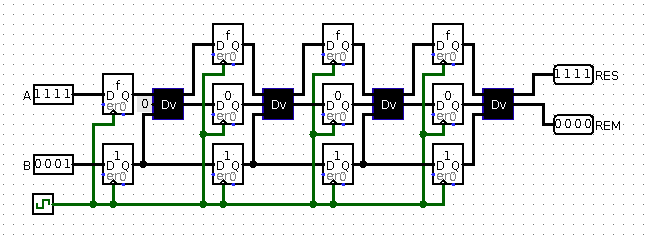
Рис 10. Реализация конвейера
И наконец, последний рисунок 10 — конвейер, великий и могучий. Это модификация простого подключения между собой вычислительных стадии, но разделенных регистрами. Ранее об этом уже говорилось, как это работает.
Между прочим, если распространение сигнала успевает за определенный промежуток времени, к примеру, схема работает на 25 мгц и сигнал за 40 нс успевает пройти по 4 стадии за 30 нс, то можно в схему добавить регистры через каждые 4 стадии, например. Допустим, для 32-х битного числа потребуется лишь 8 тактов, чтобы вычислить, что ускоряет время загрузки конвейера и получения конечного результата.
Качнуть упрощенную схему.