§ Начало рассуждений

Давно уже хотел написать статью по этому поводу и все никак руки не доходят. Пришло время описать принцип действия модуля нормализации целого числа. Вся проблема в том, что надо каким-то образом найти то количество знаков после запятой, где начинается единица. Например, есть двоичное число, которое состоит из 8 бит — 00001110 (14 в десятичной системе счисления). Задача в том, что быстро отыскать самую старшую единицу.

§ Простой способ

Это просто начать искать по одному, то есть, считать нули. Как видим, там четыре нуля, а следовательно, 5-м числом уже идет единица. Считать нули легко и приятно, но для компа это просто пытка. Если сделать простой подсчет по одному нулю, то так можно потратить кучу тактов. А как же сделать поиск гораздо быстрее?
На помощь приходит бинарная логика. Все очень просто. Мы начинаем искать группой. Если количество бит, которым оперируем, кратно 2, то есть, к примеру, 8 или 16 или 32 и так далее, то первая группа нулей на проверку будет именно половина от количества бит.

§ Другой способ

Вот сейчас проверим на примере. Возьмем число 0000001110101110. Это 16-битное число и надо вычислить количество лидирующих нулей, чтобы определить, где же находится старшая единица. Если дано 16 битное число, то проверим первые 8 бит: 00000011. Как видно, в первых 8 битах затесались две единицы, что говорит о том, что количество нулей гарантированно меньше чем 8, а это лишь означает что теперь берем первые 4 бита на проверку 0000. И там нули, что очень хорошо!
Теперь, сдвигаем наше число на 4 бита влево:
0000001110101110 — было
001110101110 — стало
Так как уже продвинули на 4 бита влево, то это означает, что могут остаться либо 2 нуля, либо 1 ноль, либо вообще ничего. Почему не может снова остаться 4 нуля? Все дело в том, что если бы там осталось 4 нуля, то это значит, что на предыдущем шаге оставалось бы 8 нулей, так как из 8 вычли 4. Так что в любом случае количество нулей слева гарантированно будет меньше чем 4.
Итак, следующий шаг. Проверим, отсталось ли 2 нуля слева? Да, там два нуля и осталось. Двигаем налево:
001110101110 — было
1110101110 — стало
Ну и проверяем, остался ли еще один нуль слева? Нет, там единица. Алгоритм закончился. Отсюда вывод: чтобы полностью проверить все 16 бит на лидирующие нули, потребуется только 4 шага, что гораздо быстрее чем 16 шагов. На самом деле, для 32 бит потребуется 5 шагов, для 64 потребуется 6, то есть сложность алгоритма получается O(logn).

§ Хитроумная схема на логисиме

Нет времени объяснять, просто оставлю это тут.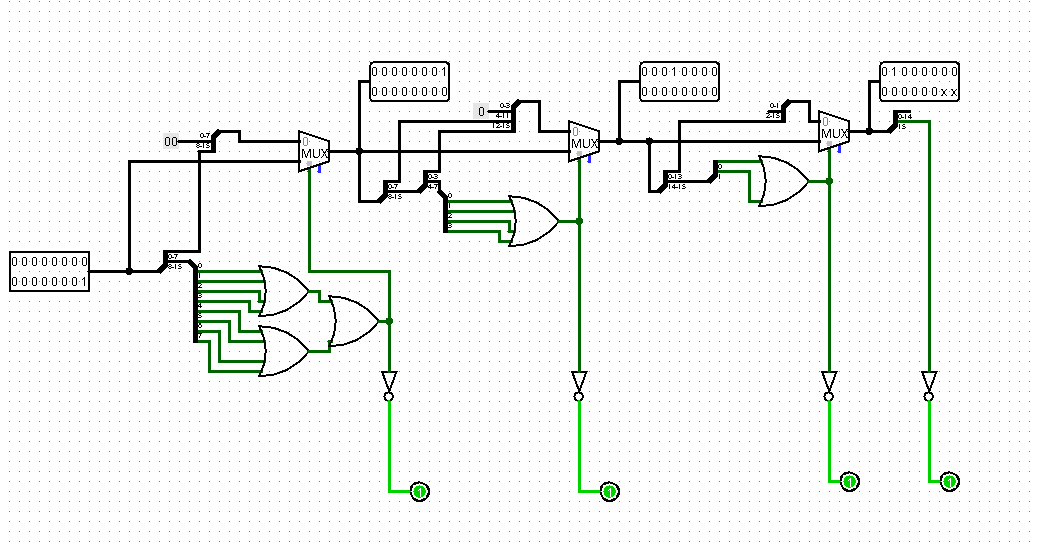

Эта схема не только показывает количество сдвигов, которое необходимо сделать, чтобы нормализовать число, но и также сразу же на лету и нормализует число.