§ Двоичное число

Как нам всем известно со школьной скамьи, в компьютере — двоичная система счисления, и это означает, что там может быть только либо 0, либо 1 и ничего более, поэтому так система счисления и называется — двоичная. Еще эта система счисления позиционная, что означает, что каждый двоичный разряд в двоичном числе занимает строго отведенное ему место.
Для начала, рассмотрим как ведется счет чисел в двоичном и десятичном виде:

BIN Десятичное
000 0
001 1
010 2
011 3
100 4
101 5
110 6
111 7

Из таблицы понятно, что двоичное число занимает 3 разряда, а вот десятичное - всего лишь 1 разряд. Получается, что для представления числа в двоичном виде требуется большее количество разрядов.
В трехразрядное двоичное число можно уместить 8 различных вариантов и комбинации, чтобы они не повторялись. В двухразрядное можно лишь поместить 4 комбинации, ну а в 1 разряд, естественно, только 2 комбинации.
Причем, если попытаться составить максимальное возможное количество комбинации 4-х разрядов, то выйдет вдвое больше, то есть, 16. Для 5 разрядов - 32, для 6 - 64 и так далее, количество комбинации каждый раз увеличивается вдвое и это понятно — ведь если добавить еще разряд, то там может быть либо 0, либо 1, то есть, это можно представить вдвое большее количество наборов, чем было до этого.
Чтобы точно знать, сколько можно представить чисел в n разрядов, надо перемножить 2 это количество раз n. Например, n=4 разряда, будет 2*2*2*2=16. В математике есть такая функция, которая называется показательной, или еще ее называют степень, которая выглядит как , то есть, это количество раз, которое надо умножить на 2.

§ Числовой циферблат

А теперь допустим, что у нас есть 4 разряда и больше нет. Да, представим то, что есть 4 лампочки, которые надо последовательно зажигать от 0 до 15, потому что число 15 - это последнее возможное число для 4-битного числа. Причем, очень важно сообщить, что последнее возможное число в n-разрядном числе будет равно , то есть, нужно возвести двойку в степень, равную количеству разрядов и вычесть единицу из него. Так, к примеру, последнее число для 3-х битов будет равно 7 (или 111), для 4-х битов будет равно 15 (или 1111), для 5 будет 31 (или 11111) и так далее.
Обращу пристальное внимание, что таким числом в двоичной системе всегда будут все единицы. Никаких исключений. А почему так? Все очень и очень просто - если добавить +1 ко всем единицам, то по ним пройдет полный перенос и они превратятся во все нули и плюс перенос в старший разряд.
А что если, если этого старшего разряда нет?! То есть после добавления 15+1 (или 1111+1) будет 0! Да, потому что некуда вместить этот старший разряд и поэтому все обращается в 0 и начинается сначала. Это явление называется числовым кольцом.
Если было 5 разрядов, то последнее число было бы 31, и после прибавления 31+1 стало бы равным 0. И это правило работает для всего, главное, это указать, сколько разрядов используется для хранения числа.
Теперь же давайте попробуем представить отрицательные числа на таком циферблате. Что такое отрицательное число? Это всего лишь положительное число, которое вычли из нуля:
Казалось бы, все очень просто понять, но ведь надо учесть, что у нас количество разрядов ограничено. Конечно, можно было бы хранить отрицательное число, добавляя, к примеру, знак. Например, перед числом писать 0 - это плюс, или 1 - это минус. Так, в принципе, числа и хранятся в разных форматах, но не в этом случае. Сейчас я расскажу о числах, которые хранятся в так называемом дополненном коде, который компьютеру намного проще вычислить.
Представим, что стрелка циферблата указывает на 0. Что будет, если добавить +2? Нужно сдвинуть стрелку на 1, потом еще на 1 вправо. Теперь стрелка указывает на 2. Добавим еще 3. Сдвигаем на 3 вправо, получаем 5. А теперь вычтем число 6! Крутить будет 6 раз влево. Теперь повернем 5 раз и стрелка указывает на 0. А что дальше будет? Нужно же еще раз повернуть влево, и куда будет указывать стрелка?
Если это 4-х битное число, то предыдущее значение будет равно 15 (или 1111). То есть, если повернуть стрелку направо, то получится число 15. Да, все так просто.
То есть, чтобы получить число -1 в дополненном коде, надо сдвинуть стрелку, которая стоит в позиции 0, на 1 влево и она переместится на последнее число, которое возможно в той битности, в которой сейчас работаем. Чтобы получить число -2, надо сдвинуть еще на 1 влево и так далее.
Давайте попробуем:

-1 | 1111 | 15
-2 | 1110 | 14
-3 | 1101 | 13
-4 | 1100 | 12
-5 | 1011 | 11
-6 | 1010 | 10
-7 | 1001 | 9
-8 | 1000 | 8

Как можно заметить, я не стал показывать -9, потому что, формально, это число уже не является отрицательным в дополненном коде. Число считается отрицательным, когда старший разряд в числе равен 1 и положительным, если 0. Если бы мы попробовали представить -9, то это было бы число 0111 (7) в двоичной системе. В таких случаях говорят, что произошло знаковое переполнение (overflow). Но эта информация пока не играет роли.
Как же определить, какой дополненный код соответствует отрицательному числу? На самом деле, все очень просто.

• Сначала, надо узнать, для скольких разрядов будем составлять дополненный код, например n=3.
• Получаем максимальное большое количество комбинации из этого кода, то есть = 8
• Вычитаем из 8 нужное число, например, 3
• Получаем 5, что является -3 в 3-х разрядном числе

§ Вычитание через сложение

Со времен школьной математики широко известно, что:
То есть, чтобы вычесть, надо сложить число с отрицательным числом. То есть, задача заключается только в том, чтобы получить это отрицательное число. Как это быстро и эффективно сделать на логических схемах?
Оказывается, путь есть! И он невероятно простой и эффективный.
Дело в том, что отрицательное число получается так:
То есть, для n-разрядного числа вычитаем нужное нам число b и получается дополненный код. А что, если сделать так?
Ничего же не поменяется? То есть, ну добавили единицу, ну вычли... Но зачем? А давайте переставим слагаемые:
Ух ты, а тут получилось — то есть то, о чем я ранее говорил, это выражение будет выдавать всегда только одни единицы и ничего, кроме единиц. Это хорошо! Просто почему это хорошо? Потому что из такого числа легко вычесть любое число. Допустим n=4, значит что является 1111 в двоичной системе счисления. Вычтем из него число 6 (0110):

 1111
-0110
-----
 1001

Вычитаем в столбик. Так, начинаем справа, 1-0 = 1, потом 1-1=0, потом 1-1=0, потом 1-0=1. Всего получается, что может быть ровно 2 случая:

1-0=1
1-1=0

Здесь прямо напрашивается вывод, что если 0 то 1, а если 1 то 0 — обычный инвертор. Значит, даже делать ничего особо не надо, надо лишь просто инвертор поставить и будет вычитаться из 15 число и получаться результат.
Это да. Но там еще +1 в конце, причем всегда. Значит, выходит, чтобы вычесть число, надо сделать так:
И тогда будет правильный ответ. Вот это вот выражение:
Это просто инвертор, несмотря на страшную форму. А что за +1? Да это просто внешний перенос! Значит, чтобы вычесть число b из числа a, надо сложить a с инвертированным значением b и добавить внешний перенос +1. И всё!
Причем, обращу внимание на то, что если внешнего переноса не будет (там будет 0), то по итогу из a будет вычтено не только b, но и -1. Выходит, что вход внешнего переноса надо лишь только инвертировать для того, чтобы получился правильный вычитатор с заемом.
Аналогично, на выходе, если получается 1, то это означает, на самом деле, что переноса не было, и наоборот. То есть, вход, выход полностью инвертируются для того, чтобы получился правильный вычитатель.
Изобразим его на схеме в logisim:

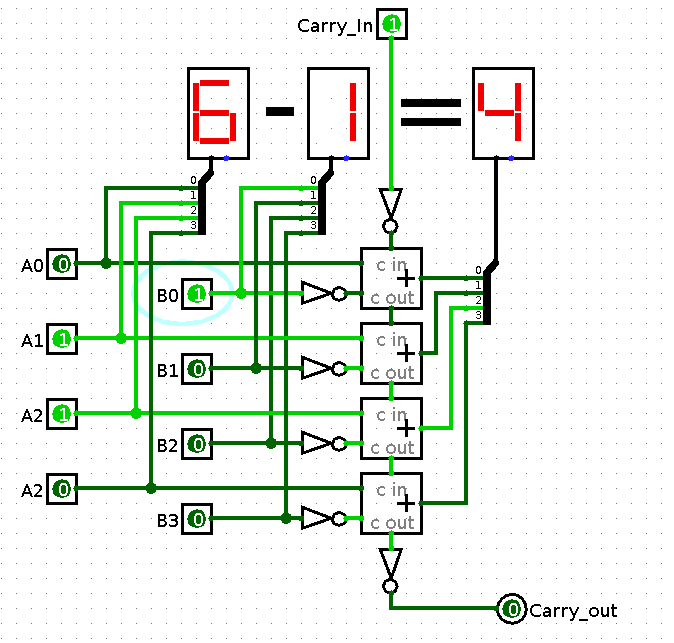
Здесь видно, что вычитается число 6 минус 1 с заемом, то есть еще -1 вычитается, и получается число 4. На выходе переноса нет, то есть 0. Если бы число получилось больше, то на выходе был бы перенос 1.