§ Повороты
Сегодня тема не будет сложной. Я позаимствую картинку из предыдущей статьи про сложение углов синусов и косинусов, потому что это все равно нам понадобится
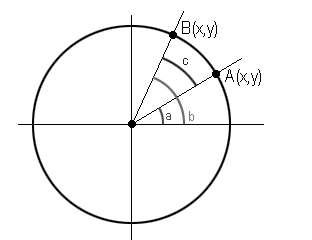
Задача такая: надо повернуть точку A на угол , чтобы из угла точка перешла к углу , или, в декартовой системе координат, из точки A в точку B.
Снова вспомнив формулы из школы, мы рассмотрим перевод из полярной системы координат в декартову
Не нужно пугаться этих формул. Здесь это длина от точки (0,0) к точке A или к точке B. Итак, вот дано у нас положение точки A, нужно повернуть на угол и получить точку B. Как это сделать? Для начала, надо понять, что точка B получается путем сложения углов и :
Здесь надо применить те самые формулы сложения синусов и косинусов
Теперь, если внимательно приглядеться, можно обнаружить, что легко можно поменять на , а на :
Здесь
Всё! Эта мегаформула используется где только можно, где только нужно, так что все нормально, все будет хорошо. Можно поворачивать сколько угодно раз и по всем возможным осям без зазрения совести.