Оглавление
§ Начало
Приве-е-е-ет! Задача состоит в том, чтобы рассчитать, например, чему равен . Для этого придется рассмотреть окружность, у которой радиус равен единице (1), то есть, единичную окружность. Были треугольники – стали окружности, рассмотрим одну из них.
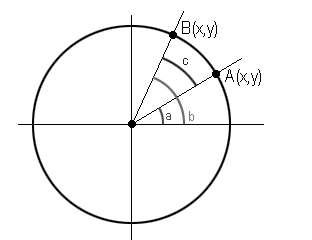
Из школьного курса математики мы знаем:
Если что, это просто определение синуса и косинуса, которое гласит, что:
Радиус у нас единичный, а – прилежащий катет, – противолежащий.
Обратим внимание, что если сложить углы , то в итоге получаем угол , либо так . Что это дает? Надо просто вспомнить, что такое угол , а именно, это скалярное произведение двух векторов и (учитывая, что они единичные):
Всё! Все доказано, расходимся.
§ Где все остальное?
Мы доказали вычитание углов для косинуса, а как же другие формулы, где синусы? Сложение? Давайте
разбираться. Для начала, попробуем вывести формулу сложения углов косинуса . Тут все просто, нужно лишь сделать и получится:
Зная, что , и , получим
Либо, в общем виде
Теперь ко всему остальному. Известно, что:
Допустим, надо сделать так:
Тут немного раскрыть и переставить скобки, то получится так:
Заменив:
Получаем
Если сделать , то тогда
§ Итоги
Теперь, что у нас вышло:
§ Умножение
Давайте докажем еще кое-какие важные соотношения. Рассмотрим, чему будет равно выражение:
Применяя доказанные выше соотношения, имеем следующее:
Вычитая один из другого получаем
То есть, другими словами
Точно тем же самым методом можно рассчитать и другое соотношение