Лисья Нора
07:12
Главная » Математика » Площадь фигур через интеграл

Оглавление


§ Площадь треугольника

Сегодня пойдет разговор про вычисление различного рода объемов, площадей через интегралы. Мне показалась эта тема достаточно интересной и любопытной, и я захотел ее просто так рассмотреть, хотя никакого практического смысла она не имеет.
Для начала рассмотрю классический треугольник и как подсчитать площадь через формулу вычисления площади прямоугольных треугольников
int3.png
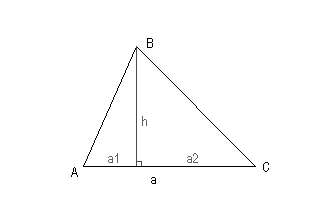
Есть высота h и основание a . Треугольник состоит из двух прямоугольных треугольников с катетами a_1 , a_2 и h . Формула вычисления площади прямоугольного треугольника простая S=\frac{ab}{2} . Подставим нужные значения S_1 = \frac{a_1h}{2} и S_2 = \frac{a_2h}{2} . Сложим S = S_1 + S_2 = \frac{1}{2}(a_1 + a_2)h = \frac{1}{2}ah . Все доказано, собственно. Другим словами, получается что вычисление площади любого треугольника – это умножение его основания на высоту и деление на 2, тоже самое что вычисление площади прямоугольного треугольника.
int4.png
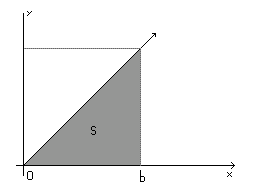
А теперь рассчитаю через интеграл. Определенный интеграл – это площадь функции от a до b . Поскольку считаем треугольник, то считать будет прямоугольный треугольник, как ранее и было выведено. То есть, в точке x = 0 будет 0, а в точке x = h значение должно быть a (основание). Будет взят определенный интеграл \int_{0}^{h} f(x) dx . Функция, которую будем считать это f(x) = \frac{ax}{h} . Действительно, если x = 0 то f(0) = \frac{a 0}{h} = 0 , и f(h) = \frac{ah}{h} = a . Условия соблюдены.
S = \int_{0}^{h} \frac{ax}{h} dx = \frac{ax^2}{2h} |_{0}^{h} = \frac{ah^2}{2h} = \frac{1}{2}ah
Вот и все, что надо было знать про треугольники.

§ Объем прямоугольной пирамиды

На самом деле, объем пирамиды считается точно тем же самым способом, что и считается площадь треугольника, просто изменяется функция подсчета. Для пирамиды в ее вершине, как и треугольнике, должна быть f(0) = 0 , но в основании функция должна принять вид f(h) = a^2 , площадь квадрата. Но функция получается не совсем линейная. В точке x = \frac{h}{2} функция должна описывать S(\frac{h}{2}) , получается что f(x) = S(x) на самом-то деле. Значит, получается так S(x) = x^2 . Но нам нужно сделать так, чтобы в x = h было S(h) = a^2 , поэтому итоговой функцией будет f(x) = \frac{(ax)^2}{h^2} . Проверим. Очевидно что в x = 0 будет 0. Теперь проверим, что будет при x = h :
f(x) = \frac{(ah)^2}{h^2} = \frac{a^2h^2}{h^2} = a^2
Все верно. Считаем интеграл:
V = \int_{0}^{h} \frac{(ax)^2}{h^2} dx = \frac{a^2x^3}{3h^2} |_{0}^{h} = \frac{a^2h^3}{3h^2} = \frac{1}{3}a^2h
Причем тут a^2 – это именно основание пирамиды, и оно может быть вообще любым. Так что можно переписать следующим образом и это будет правильно:
V = \frac{1}{3}Sh

§ Длина окружности

Круг – это весьма загадочное явление в математике. Длина окружности с радиусом 1 будет равна 2\pi , например. Как это доказать? Я не знаю точно, но если попробовать начать измерять длину окружности, то скоро будет заметно, что отношение длины окружности к радиусу будет равно как раз этому 2\pi .
То, как выводится длина окружности, существует множество доказательств. Но я тут доказывать не буду, потому что нет смысла. Могу лишь сказать, что длина окружности зависит от радиуса и равна 2\pi r где r – это радиус.
Скажу не к месту, но самое близкое приближение к числу \pi это отношение \frac{355}{113} . Оно было найдено в Древности и до сих пор никем не переплюнуто. Это самое короткое из самых возможных и точных сокращений. Потрясающе!

§ Площадь круга интегрированием

Начну (и закончу на этом) с самого легкого – интеграла. Интеграл это сумма бесконечно малых величин, и потому можно окружность поделить на треугольники со стороной к примеру dt и высотой r . Чтобы найти площадь этого треугольника, достаточно взять интеграл:
\int_0^{2\pi r} \frac{1}{2} r dt = \frac{1}{2} r t | _0^{2\pi r} = \frac{1}{2} r 2\pi r - 0 = \pi r^2
Вот и все доказательство.
Доказательства получше можно в [[https://ru.wikipedia.org/wiki/Площадь_круга Википедии]] прочесть.

§ Площадь сектора

Вот как раз для этого статья и писалась. Если мы берем сектор длиной 2\pi , то тогда этот сектор будет равен площади окружности, потому что этот сектор и есть окружность. Значит, если взять сектор длиной \pi , то в таком случае, он будет равен половине окружности. Из этого видно, что если a – это длина сектора в радианах, то \pi r^2 \frac{a}{2\pi} . Сделаю сокращения для числа \pi , и получится S = a \frac{r^2}{2}

§ Объем шара

Чтобы получить объем шара, достаточно проинтегрировать от -r до r все площади круга на этом участке. Получается что-то типа нарезания сендвича из очень маленьких кругов.
Радиус каждой окружности будет подчиняться следующему правилу:
y = \sqrt{r^2 - x^2}
Где y – это радиус окружности в точке x. Соответственно, вместо r в площади окружности подставляется y :
\pi r^2 = \pi (\sqrt{r^2 - x^2})^2 = \pi (r^2 - x^2)
Осталось только проинтегрировать от -r до r:
V = \pi \int_{-r}^r (r^2 - x^2) dx
Интегрируем это дело:
\pi \int_{-r}^r (r^2 - x^2) dx = \pi (r^2 x - \frac{x^3}{3})|_{-r}^r
Первая часть определенного интеграла:
r^2 x |_{-r}^r = r^2 r - r^2 (-r) = r^3 + r^3 = 2r^3 = \frac{6r^3}{3}
Я намеренно сделал умножение на 3, это будет нужно после вычисления второй части интеграла:
\frac{x^3}{3} |_{-r}^r = \frac{r^3}{3} - \frac{-r^3}{3} = \frac{2}{3}r^3
А теперь все в кучу складываю:
V = \pi \int_{-r}^r (r^2 - x^2) dx = \pi (\frac{6r^3}{3} - \frac{2 r^3}{3}) = \frac{4}{3} \pi r^3
Доказывать интегралами очень весело, когда ты понимаешь, что ты делаешь.