Оглавление
§ Один нейрон
Всегда надо начинать с простого, поэтому начну разговор с одного, единственного искусственного нейрона в составе перцептрона, разберу то, как он работает. Ранее было рассказано, как работает нейрон и почему он именно так работает.
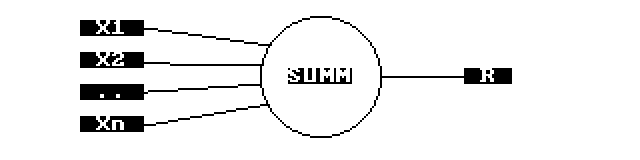
Схематически, нейрон выглядит следующим образом:
- На вход подаются некоторые значения с внешнего мира, либо с выходов предыдущих нейронов
- В нейроне умножаются веса каждого ребра на значение этого ребра
- Сумма проходит через функцию активации, к примеру, сигмоиду
- Результат появляется на выходе нейрона и распространяется либо дальше, либо является окончательным
Один нейрон способен классифицировать данные, разделяя их по обе стороны плоскости, однако, он способен лишь разделять на две части, но если задача становится посложнее, чем просто разделить области на две части, то необходимо добавлять еще нейроны. Обычно любая нейросеть, которая состоит из нейронов, многослойная, поскольку решение почти любой задачи всегда требует результатов с предыдущих слоев нейронов.
§ Решение задачи XOR
Как известно, решить задачу XOR с помощью одного нейрона не представляется возможным, поскольку нет такой прямой линии, которая бы разделила 3 региона сразу, а XOR именно состоит из 3-х регионов. Это легко увидеть, если посмотреть на расположение точек на графике, который отображает таблицу истинности XOR.
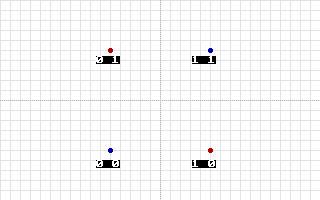
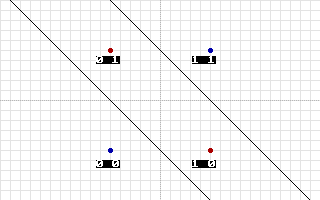
Здесь точки красного цвета означают, что в этом месте функция должна быть больше чем 0, а точки синего – меньше 0. Как бы не пытаться проложить линию, она никогда не сможет рассечь плоскость надвое так, чтобы результаты были правильными. Единственным правильным решением будет рассечь плоскость на 3 области с помощью двух линии, как показано на второй иллюстрации.
Для начала сделаем попытку создать функцию с помощью простой булевой алгебры. Чтобы получить такую таблицу, потребуется скомбинировать несколько других функции. Составлю для них собственные таблицы истинности:
A B | NAND | OR | AND | XOR
0 0 | 1 | 0 | 0 | 0
0 1 | 1 | 1 | 0 | 1
1 0 | 1 | 1 | 0 | 1
1 1 | 0 | 1 | 1 | 0
Итак, как видим, чтобы получить XOR, необходимо будет выполнить 3 действия:
- N =
A nand B - O =
A or B - XOR =
N and O
Каждое действие задействует 1 нейрон, а это означает, что получится архитектура из 3х нейронов. Для решения и упрощения задачи, я буду использовать ступенчатую функцию активации, а не сигмоиду, хотя и она тоже будет работать, но зачем сейчас усложнять?
- Нейрон 1: Функция NAND описывается через уравнение
s(x) = 1 – x – y, поэтому веса будут, соответственно (-1,-1,+1), т.к. при x находится -1, при y находится +1, и свободный коэффициент равен +1; - Нейрон 2: Функция OR задается уравнением
s(x) = x + y + 1, поскольку s(x) отрицательное только в случае x=-1, y=-1, веса у этого нейрона (+1,+1,+1); - Нейрон 3: Функция AND описывается ровно так же, как и NAND, просто везде меняется знак
s(x) = x + y – 1(+1,+1,-1); это легко проверить, т.к. s(x) будет больше чем 0 только тогда, когда x=1, y=1
Получается, что для того чтобы описать работу логических функции, достаточно правильно задать архитектуру сети (топологию), и указать у каждого нейрона собственные весовые коэффициенты.
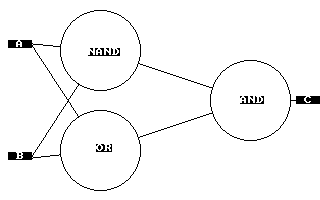
Теперь можно считать, что XOR реализован в нейросетях.
§ Слои
У нейросетей есть слои, которые обычно называются так:
- Входной – это нейроны, которые находятся непосредственно на приеме внешних данных
- Скрытый – слои нейронов, которые получают результаты от предыдущих нейронов и передают эти результаты следующим
- Выходной – непосредственно, слой нейронов, получающие данные либо с входного слоя, либо с внешних данных, либо же со скрытого слоя и являющиеся уже результатом
У нейросетей может быть очень много вариантов архитектуры. К примеру, помимо обычного нейронного слоя, существуют также рекуррентные нейросети, сверточные. Все они отличаются только тем, как присоединены ко входам и друг к другу. От выбора архитектуры может зависеть результат и свойства нейросетей, про то, как их конструировать, как их обучать, написаны книги, талмуды и целые библиотеки. В одной крохотной статье я не смогу выразить даже сотые доли процента того, что уже написано по этой теме.