12:08
Ханойская башня — Лисья нора
§ Легенда
Однажды буддийские мудрецы Древности в славном городе Ханое поняли, что Брахма им не помеха и сказали ему, чтобы он шёл своей дорогой. Но Брахма был в ярости от нахальства мудрецов и воздвиг огромные три стержня толщиной ровно с пчелу (обращаю внимание, что не ханойского комара), и высотой несколько локтей среднестатического человека по всей Земле. На один стержень он положил 64 диска из чистейшего золота без примесей, отчего у мудрецов резко загорелись глаза, чтобы распределить их по своим карманами и быть таковыми, на что Брахма сказал, что если они это сделают, то их тут же испепелит кара небесная. Естественно, никто слушать его не стал и пару-тройку дерзких брахманов были испепелены. Остальные не стали испытывать Судьбу, иметь дело с Брахмой — себе дороже.Сказал Брахма следующее: "Переложите все 64 золотых диска, но так, чтобы ни снизу были диски толще, чем сверху, и перекладывать вы будете по одному. Кто ослушается — того испепелит Кара Небесная". Никто не знал Кару в лицо, но увидели результат и побоялись ослушаться. Но некоторые молодые смельчаки все-таки хотели увидеть Кару воочию и перекладывали сразу по два, но были испепелены прежде, чем смогли унести себе домой эти листы из чистого золота.
И тут один робкий брахман по имени Самисвами спросил: "А что нам будет, если мы перенесем со стержня А на стержень Б"? На что Брахма, улыбнувшись, ответил "Тот, кто первым это сделает, обретет все эти золотые диски единолично".
С тех пор говорят, брахманы так и перекладывают эти листы. Прошло уже тысячу лет, а они перекладывают. Там уже целые династии перекладывальщиков образовались. Никто не помнит, зачем они это делают, но перекладывают и перекладывают. Уже и с помощью роботов это делают, но все равно не успевают к дедлайну.
Теперь вопрос: сколько эти люди будут туда-сюда гонять золотые диски?
§ История
То что сверху я сочинил, это чистого рода моя фантазия и, конечно же, ничего и в помине не было такого. Красивая сказка, да еще и пересказанная неверно. Знакомство мой с этим алгоритмом произошло, как и обычно со всеми, в детстве, примерно в 9 лет, когда я увидел ее в какой-то интересной книге по Бейсику. Там эта Ханойская башня выставлялась как пример красивого рекурсивного алгоритма. Конечно, я ничего не понял.Спустя лет 20-25 наконец-то мне удалось разобраться с алгоритмом и это оказалось... просто элементарно! Как я не мог понять такие очевидные вещи?
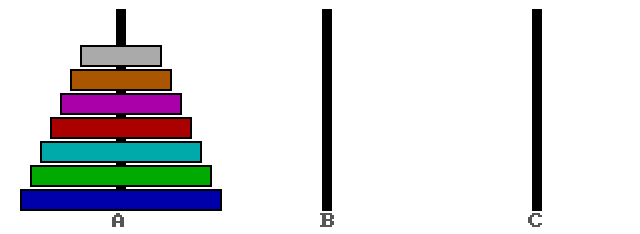
Рис 1. Ханойская башня высотой 7 листов
§ В чем же суть идеи?
Все очень и очень просто. Чтобы перенести башню с A на B, надо сделать следующее:Шаг 1
Взять всё, что лежит на широком диске и переложить его со стержня А на стержень C.
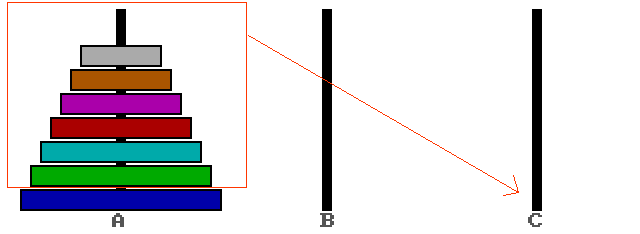
Рис 2. Перекладываем 6 листов с А на C
Получается вот так:
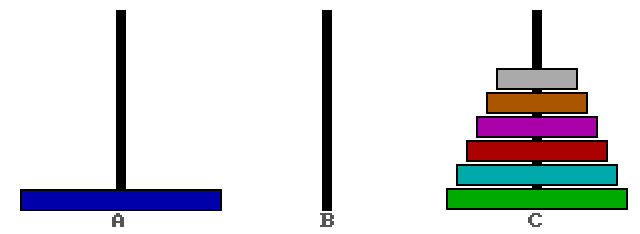
Рис 3. Состояние стержней после того, как переложили с A на C
Шаг 2
Переложить самый широкий с A на B:
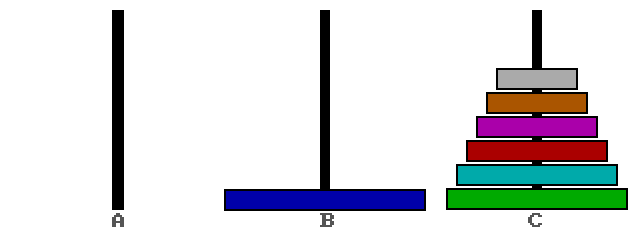
Рис 4. Перекладываем с А на B
Шаг 3
Переложить обратно всю башню, что находится на C (там 6 листов), на B:
Рис 5. Перекладываем с C на B
Вот и всё! Больше ничего не надо, только это.
§ Но мы нарушили правила!
Именно. Мы нарушили правила, но не все так просто. Дело в том, что это — общая схема для алгоритма. Суть идеи. А для того, чтобы правила не были нарушены, надо сделать следующее. Когда мы начинаем перекладывать более чем 1 плашку, мы должны повторить тот же самый алгоритм, но для более меньшей (на одну меньше) башней.Это — рекурсия.
Как так получается? Давайте рассматривать на простом примере из 3-х плашек.
= | | === | | ===== | | A B CТеперь попытаемся переложить с А на B. Так просто не выйдет. Для начала, мы должны переложить две плашки сверху с A на C. Представим, что нижнего слоя нет, и нам надо переложить с A на C:
= | | === | | A B CШаг 1. Перекладываем A -> B
| | | === = | A B CШаг 2. Перекладываем A -> B
| | | | = === A B CШаг 3. Перекладываем B -> C
| | = | | === A B CКак видим, мы справились ровно за 3 шага. И правда, получилось полностью переложить башню с A на C!
Алгоритм устроен следующим образом. Если мы хотим переложить башню с A на B, то тогда надо использовать C как вспомогательный штырь. Пример:
- Сначала кладем A -> C (вспомогательный)
- Потом, собственно с A -> B
- И со вспомогательного C -> B
Зная это, я напишу процедуру на Си:
void move(int a, int b, int c) { printf("%d -> %d", a, c); printf("%d -> %d", a, b); printf("%d -> %d", c, a); }Тем самым, например, вызвав процедуру с параметрами
move(1,2,3), будет выдана следующая последовательность:1->3
1->2
3->2
§ И наконец, алгоритм
А теперь — самое интересное, ради чего вся эта статья и писалась. Как я говорил ранее, перекладывание башни, у которой более чем 1 лист, например, башню 2 листа, надо переложить саму. Это значит, что надо вызвать процедуру перекладывания именно для нее.Я модифицирую код
move, добавив туда значение n - а именно, какую высоту башни мы переложим. Если высота будет n = 1, то будет напечатана процедура перекладывания одного элемента с исходного штыря номер A на требуемый штырь номер B, если же n > 1, то для того чтобы переложить с основного на вспомогательный штырь, а также со вспомогательного на тот, куда перекладываем, будет вызываться... опять процедура move, но с уже меньшим количество листов на 1.void move(int a, int b, int c, int n) { if (n == 1) { printf("%d -> %d\n", a, b); // Просто перекладываем с одного на другой штырь } else { move(a, c, b, n-1); // Перекладываем башню с A -> C, вспомогательный B printf("%d -> %d\n", a, b); // Здесь просто сообщаем, что переложили с A -> B (1 лист) move(c, b, a, n-1); // Перекладываем C -> B, вспомогательный A } }Как ни странно, но это и правда весь алгоритм. Процедуру можно немного сократить, если не вызывать перекладывание башни из 1 листа:
void move(int a, int b, int c, int n) { if (n > 1) move(a, c, b, n-1); // Перекладываем башню с A -> C, вспомогательный B printf("%d -> %d\n", a, b); // Сообщаем о перекладывании одного листа A -> B if (n > 1) move(c, b, a, n-1); // Перекладываем C -> B, вспомогательный A }Итак, для того, чтобы получить последовательность перекладываний башни высотой, например, 3, с 1-го штыря на 2-й, используя в качестве вспомогательного 3-й, надо вызвать функцию
move(1,2,3,3), на что получим краткий ответ 1->2, 1->3, 2->3, 1->2, 3->1, 3->2, 1->2. Это ровно 7 действий.§ Ну и сколько будут перекладывать монахи 64 листа?
Почему получилось именно 7, когда высота башни будет 3? На самом деле, это получается потому, что получается двоичное дерево. Допустим, высота башни 3. Это значит, что, зайдя в функцию move, будут два раза вызваны move, которые перекладывают сначала на вспомогательный штырь, а потом с него на необходимый.Первый уровень вызывает 2 уровня ниже. Дочерние два уровня вызовут тоже два раза перекладывание, что дает уже 4 ветки. И теперь, каждая из этих веток, вызовет 4 раза printf. Но не стоит забывать, что вышестоящие уровни вызовут printf тоже, но уже 2 раза! И конечно же, корневой уровень вызовет prinf 1 раз.
В сумме 1+2+4=7. Это сумма геометрической прогрессии с шагом 2, а значит (выводить формулу не буду), количество шагов перекладывания будет равно .
Что же, теперь долгожданный ответ, шагов надо сделать, чтобы переложить всё. Сколько монахи будут перекладывать? Допустим, если они делают 30 перекладываний в секунду с помощью роботов, конечно же, то через 19 498 080 579 лет (19 млрд) может и закончат... если повезет.