12:00
Пирамидальная сортировка — Лисья нора
§ Про пирамиды
Однажды строил пирамиду известный на всю округу сатирик и комик, и его звали Хеопс, парни еще его звали Хуфу, или Хнум-Хуфу, кому как было веселее. И вот вышел он на сцену и говорит "Я такую пирамиду создам, что вы ахнете". Его сначала тухлыми помидорами с финиками и фенеками забросали, но он не растерялся и сказал, что каждый овощно-плодовый продукт, который в него влетел, будет роздан бедным слоям населения, отчего все приутихли и стали думать. Путем голосования и жеребьевки все решили, что Хеопс достоин быть монархом Айгюптоса, впряглись и стали таскать многотонные блоки на вершину.Вопрос: зачем я это все написал? Ответ: потому что пирамида имеет пирамидальную форму и самая высокая часть в ней всегда наверху. Логика: ее нет.
§ Как хранить пирамиду
В холодильнике.А если более серьезно, то надо сначала рассказать о том, что это за пирамида такая, что с ней делать и как дальше жить. Пирамидальная сортировка отличается от других сортировок тем, что она очень стабильная и выполняется всегда за одинаковое время при любом раскладе элементов. Именно при раскладе, а не количестве. Чем больше количество элементов, которые надо сортировать, тем больше и время, которое надо потратить на это дело. Интересный факт в том, что сложность алгоритма составляет , где число n — это количество элементов в пирамиде, а это, условно говоря, количество шагов или сравнений.
Теперь расскажу о самом устройстве пирамиды. На ее верхушке всегда находится один элемент, который всегда имеет либо самое большое, либо самое малое значение из всей пирамиды полностью. И это всегда так. Если это не так, то делаются действия, чтобы это опять стало так. Суть пирамидальной сортировки в том, чтобы раз за разом извлекать с верхушки пирамиды самый большой оставшийся в пирамиде элемент, который там всегда будет. Вы спросите, а это там постоянно будет самый большой элемент? Об этом поговорим позже.
Верхушка пирамиды состоит из одного элемента, однако, она имеет ровно два потомка, которые либо меньше по значению, чем родитель, либо меньше — и никак иначе! Если это не так, то структура пирамиды считается нарушенной и требует мгновенного восстановления справедливости. Иначе мы сортировать не сможем.
Как можно догадаться, каждый из потомков имеет еще 2 потомка, те — еще два и так до тех пор, пока пирамида не будет заполнена до самого основания. Легко понять, что количество элементов в каждом слое пирамиды увеличивается на 2, по геометрической прогрессии, то есть, в первом слое будет 1 элемент, во втором слое — 2 элемента, в третьем — 4, в четвертом — 8 и так далее. Нижний слой может быть заполнен не до конца, если количество n элементов пирамиды не кратно степени двоек.
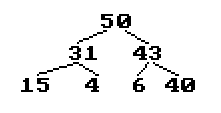
На рисунке представлена простая пирамида на 7 элементов, из 3-х слоев. Эта пирамида полностью сохраняет свойства двоичного сортирующего дерева, а именно — у родителя всегда два потомка и каждый из этих потомков меньше или равен родительскому.
Как же хранить это дерево? Все очень просто. Представим то, что есть массив
arr[]. Самый верхний элемент будет расположен в arr[0]. Да следующих элемента расположены в arr[1] и arr[2]. Третий слой располагается в элементах arr[3], arr[4] и arr[5], arr[6]. И так далее.Интересная особенность такого хранения пирамиды заключается в том, что очень легко и удобно можно найти двух потомков. Если взять любой узел пирамиды , то левый потомок будет располагаться в узле а правый в .
§ Как уже начать сортировать?
Конечно, для того, чтобы начать сортировать, надо сделать так, чтобы пирамида отвечала нужным требованиям, а именно — чтобы любой родитель был старше своих двух потомков и выполняться это требование должно для всех узлов пирамиды. Но, чтобы упростить дальнейшие разъяснения, допустим то, что пирамида кем-то уже была правильно выстроена и нам нужно только лишь ее отсортировать. О том, как ее выстроить, я расскажу позднее. Это не такое сложное дело, но для него требуется понять то, что буду сейчас говорить.Приведенная в порядок пирамида всегда содержит на своей вершине наибольшее число. Это происходит потому, что у каждого родителя потомки всегда младше, поэтому старший родитель (корень или верхушка) пирамиды имеет максимальное значение и это хорошо.
Делаем следующее. Мы забираем сверху это значение и обмениваем с самым последним элементом у пирамиды, то есть, наверх пирамиды ставится один из самых наименьших значений. Я сказал что это один из, потому что их может быть несколько. Поставив это значение на вершину пирамиды, мы уменьшаем саму пирамиду на одно значение. Теперь количество элементов там будет на 1 меньше, но в самом конце списка будет находится самый большой элемент пирамиды. Он перестает участвовать в сортировке, ибо уже стоит на своем правильном месте.
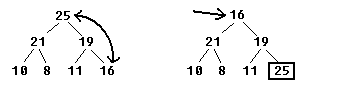
На примере показано, как происходит обмен в пирамиде. Число 16 было ранее в самом конце, и одним из самых наименьших, и теперь оно находится в корне, а 25 встало на свое место.
Однако, проблема вот в чем. Когда 16 находится в корне, оно явно находится не на своем месте, ибо нарушается порядок двоичного сортирующего дерева, так как у него два потомка и оба этих потомка старше 16.
Что делаем в этом случае? Выбираем самого большого потомка их всех и обмениваем его с корнем. Поскольку оба этих потомка были самыми большими, то больше них уже никто не может быть, если идти вниз пирамиды (что очевидно). Выбрав наибольшего из потомков, мы устанавливаем в корень самый большой элемент из всей кучи. Число же 16 в нашем случае, отправляется вместо него.
Самый большой потомок был 21, так что обмениваем с 16.
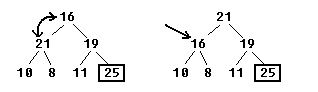
Теперь ясно видно, что 16 встало на свое место, ибо оно старше двух своих потомков и далее делать уже ничего не надо. Свойства дерева восстановлены и теперь можно сделать тоже самое, что делали ранее — берется самое большое число, а именно, 21 и обменивается с последним не отсортированным элементом в пирамиде, то есть, с числом 11.
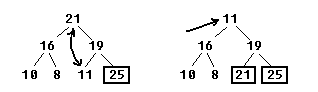
Как можно заметить, число 21 встало на свое место, перед числом 25, и это ясно заметно, что вырисовывается некая убывающая последовательность, начиная с конца. Обращаю внимание, что например, у числа 19 нет потомков больше, потому что те потомки, на которые сейчас указывается, уже не относятся к не отсортированной пирамиде.
Каждая новая итерация убирает с конца пирамиды значение и туда ставится самый большой, который остается в куче.
Все повторяется заново. Теперь мы видим, что в корне 11, а это неправильно, ибо у него есть потомки, старше корневого. Этот потомок — число 19. Обмениваем 19 с 11, и на самом деле, он встает на свое место, поскольку больше потомков у него нет.
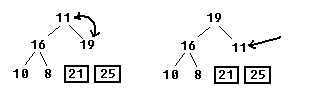
Как и обычно, значение с корня обменивается с числом 8 в конце пирамиды и получается уже последовательность 19, 21, 25. Не думаю, что стоит продолжать сортировку, поскольку принцип и так уже понятен.
Самый лучший способ понять лучше, это самостоятельно нарисовать эту пирамиду и попытаться ее отсортировать по алгоритму, что я написал выше. После того как будет отсортирован последний элемент, вместо пирамиды появится сортированный по возрастанию массив значений.
§ Приведение исходных значений в правильную двоичную кучу
Выше я рассмотрел идеальный случай, когда дерево уже сформировано для того, чтобы начать его сортировать, однако, в реальности так не может быть, чтобы правильно поставить значения сразу же. Поэтому, чтобы восстановить дерево в правильный порядок, надо сделать так, чтобы у каждого узла были потомки, младше него.На самом деле, это сделать очень просто. Нужно начать проверять узлы с предпоследнего слоя, то есть, самые дальние узлы от корня, просматривая потомков так, чтобы они вставали на свое место. Для примера, пусть будет такая пирамида:
20
15 25
23 5 51 30Начинаем просматривать предпоследний слой, справа налево, снизу вверх. Сразу же замечаем то, что тут не все в порядке, поскольку 25 меньше чем 51 и 30 и, чтобы это исправить, обмениваем 51 и 25 местами. Выбираем самого большого потомка для того, чтобы два нижних потомка были меньшего в любом случае. Данный узел был восстановлен успешно. Теперь двигаемся левее, к узлу 15. Здесь тоже, 15 меньше чем 23, и значит, надо обменять 15 и 23 местами, что восстановит свойства пирамиды на данном участке. Что теперь получится:
20
23 51
15 5 25 30Как мы видим, весь нижний слой был восстановлен успешно. Переходим к слою выше, в данном случае он отвечает за корень пирамиды. Как видно, 20 меньше и 23, и 51. Как и раньше, выбирается наибольший элемент и делается обмен, то есть, 51 меняется с 20 местами. Этот узел теперь восстановлен:
51
23 20
15 5 25 30Но это еще не все! Следим за узлом, где теперь 20, он опять нарушил свойства пирамиды и надо его снова обменять с числом 30 (наибольшим потомком):
51
23 30
15 5 25 20Алгоритм закончил свою работу и свойство пирамидальности было восстановлено. Теперь можно сортировать по тому алгоритму, который рассматривался в предыдущем параграфе.Самое интересное в том, что я смог объяснить всё про сортировку пирамидой.
§ Программная реализация
Пришло время начертить все кодом.Процедура для преобразования в двоичную кучу.
void heapify(int arr[], int n, int i) { int largest = i; for (;;) { // Инициализируем наибольший элемент как корень int l = 2*i + 1; // левый = 2*i + 1 int r = 2*i + 2; // правый = 2*i + 2 // Если левый или правый дочерний элемент больше корня if (l < n && arr[l] > arr[largest]) largest = l; if (r < n && arr[r] > arr[largest]) largest = r; // Родитель является самым большим элементом, завершить спуск if (largest == i) return; // Обмен с самым большим потомком swap(arr[i], arr[largest]); i = largest; } }Основная функция, выполняющая пирамидальную сортировку.
void heapSort(int arr[], int n) { // Построение двоичной кучи for (int i = n / 2 - 1; i >= 0; i--) heapify(arr, n, i); // Один за другим извлекаем элементы из кучи for (int i = n - 1; i >= 0; i--) { swap(arr[0], arr[i]); // Перемещаем текущий корень в конец пирамиды heapify(arr, i, 0); // Вызываем процедуру heapify на уменьшенной куче } }И основной файл
#include <iostream> using namespace std; int main(int argc, char* argv[]) { int arr[] = {12, 11, 13, 5, 6, 7}; int n = sizeof(arr) / sizeof(arr[0]); heapSort(arr, n); for (int i = 0; i < n; i++) { cout << arr[i] << " "; } cout << "\n"; return 0; }
§ Демон странция