§ Приветствую тебя, киберсущество!

Нейросети! Страшное и ужасное слово, бич современности. Сейчас нейросети используются настолько часто и настолько мощно и везде, что, будучи школьником и учеником 7-го класса, уже не составляет никакого труда сделать и обучить свою нейросеть. Эта тема, наряду с майнингом биткоинов, циркулирует в киберпространстве уже с того времени, как Сумрачный Гений смог обучить свою первую нейросеть и сделать из него гомункула современного тренда. Не зная о том, что такое нейросеть, невозможно выжить в этом жестоком мире современных технологий.

§ Искусственный нейрон

Но откуда пошла нейросеть и что она делает? Нейросеть — это не панацея от всех бед, и, как и обычно, подсмотрена из настоящей живой природы. Было сделано предположение, что можно создать искусственный нейрон на основе математического приближения к живому.
У живого нейрона есть 3 части:

• Дендриты
• Аксоны
• Сам нейрон (еще его называют сома, перикарион)

Так вот, по дендриту идет ток к нейрону, нейрон же генерирует на основе входящих в него дендритов и аксонов другой ток и передает его через исходящий от него аксон к другим нейронам, или передает его по другим дендритам. В живой природе не все так просто.
Люди решили упростить задачу и назвали такой нейрон перцептроном (приемником), и сделали так:

• Вместо дендритов — входы в нейрон (один или несколько)
• Вместо аксонов — выход из нейрона (один или несколько)
• Вместо нейрона — перцептрон, который как раз и обрабатывает входящую в него информацию

Входы нейрона - это какие-то числа от минус бесконечности до плюс бесконечности. Входами нейрона могут быть только числа и ничто иное. Поэтому, при обучении надо представлять данные в числовом виде. Картинку, аудио, текст - все должно быть числом.

§ Веса входов

Приведу иллюстрацию перцептрона: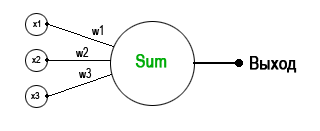

Здесь имеются 3 входа, которые называются . Они все входят в нейрон, который каждому входу назначает свой собственный вес — входу x1 назначается вес w1, входу x2 — вес w2, ну и входу x3 вес w3. Эти веса умножаются на значение входа (x_1,2,3) и все вместе они суммируются:
Тем самым образом, меняя веса, получаем линейное уравнение. Вес нужен, чтобы регулировать значимость каждого входа. Чем выше вес - тем вход значимее. Если же вес вообще отрицательное число, то входное значение вообще вычитает из общей суммы. Вес может быть и нулевым, тем самым вообще убирая вход из уравнения.
Здесь веса - это константы, которые не должны меняться со временем, поскольку суть как раз в том, чтобы обучить нейрон так, чтобы он распознавал образы, не меняя весов. Процесс же обучения нейросети - это процесс поиска весов, которые и будут потом использоваться.
Математическая запись суммы для всех весов:
Здесь n - это количество входов для нейрона.

§ Активационная функция

Простое суммирование для нейросети ничего не решает, потому что с помощью обычных сумм нельзя будет сделать то, что умеют нейросети - приблизительно распознавать образы. Так что помимо суммы элементов существует также функция активации нейрона. Что это за функция такая и для чего она нужна? Функция активации бывает разной, и нужна она для того, чтобы нейрон сработал.
Активация нужна для того, чтобы определить, достаточна ли сумма весов для того, чтобы активировать данный нейрон. Если нет - то тогда нейрон считается неактивным, а есть да - то активным. Ваш Кэп.
То есть как? Допустим у нас есть входы, которое перемножились со своими весами и выдали некий результат. Функция активации делает следующее - на выход подается +1 (к примеру), если веса получились положительными или -1, если отрицательными. Такая функция активации называется пороговой, и она обычно простая.
Здесь o - это выход нейрона, а net - это сумма входов и весом. Но для обучения перцептрона такая функция оказывается слишком "резкой" и к тому же, для нее не будет работать алгоритм обратного распространения ошибки, который будет рассмотрен далее.
Существует так называемая "логистическая функция", или сигмоида, и выглядит она так:

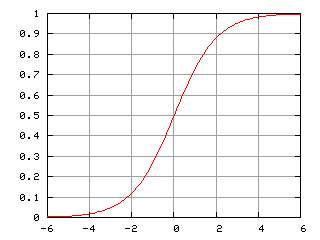
Короче говоря, формула такая:
Выбрали ее такой не случайно и я покажу далее, почему именно. Суть такая, что когда вычисляются выходы, то на самом деле выходом будет не сумма весов и входов, а еще и применена эта логистическая функция:
Вот такой вот страшный ужас выходит. То есть сумма проходит через функцию активации и уже потом идет на выход.
На этом разговор об отдельном нейроне можно завершить. Далее будем рассматривать совокупность нейронов и теорию их обучения.