§ Постановка задачи

Этот многострадальный алгоритм я постоянно забываю, и потому наконец, решился его записать, чтобы в будущем не забыть еще раз. На самом деле алгоритм работает очень просто. Начну с постановки задачи.
Задача: найти максимальное количество перестановок для заданного количества чисел от 1 до n. Пример, максимальное количество перестановок одного только элемента - это 1, двух элементов - это 2, то есть есть фишка A, фишка B - они могут поставиться так AB и BA, и больше вариантов нет. Для трех фишек это будет уже 6 вариантов: ABC, ACB, BAC, BCA, CAB, CBA. Вот теперь надо это будет найти.
Суть идеи крайне проста. Допустим есть набор фишек из 3 штук (A, B и C). Сначала мы раскладываем все варианты, которые начинаются на A: ABC и ACB. Варианты закончились. Потом все варианты, которые начинаются с B: BAC, BCA. Далее все варианты, начинающиеся с C: CAB, CBA. Получается вот так:

A - ABC, ACB
B - BAC, BCA
C - CAB, CBA

Дело в том, что функция, которая вычисляет перестановки, рекурсивная.

§ Алгоритм

Итак, на столе лежат 3 фишки, отсортированные по порядку. На фишках написаны числа 1, 2, 3. Алгоритм меняет первую фишку три раза - сначала меняет ее на 1, потом на 2, потом на 3.

[==1==]   [==2==]   [==3==]
---^

Меняем фишку 1 на 1 (по факту ничего не происходит). Далее, теперь сдвигаемся на одну позицию справа и начинаем менять фишки, начиная с 2 по 3. Работаем тем же самым способом, меняем фишку 2 на 2:

[==1==]   [==2==]   [==3==]
-----------^

Сдвигаемся еще на одну позицию направо. Мы достигли максимального значения (последняя фишка), и далее менять бессмысленно ее саму с собой уже. Выводим на экран:
1 2 3 (текущее положение фишек)
Теперь самое интересное. Возвращаемся на шаг влево и меняем уже не 2 с 2, а 2 с 3, то есть получая вот что:

[==1==]   [==3==]   [==2==]
  -----------^

Сдвигаемся направо, достигаем 3-й фишки, выдаем на экран текущее положение
1 3 2
Как можно заметить, получается, что комбинации были исчерпаны для 1. Действительно, возвращаемся на шаг назад и снова меняем 2 и 3, чтобы вернуть обратно исходное положение.
С позицией 2 полностью все исчерпано. Вернемся к позиции 1. Там менялся 1 с 1, а теперь будет меняться 1 с 2, получая вот такое:

[==2==]   [==1==]   [==3==]
---^

Как видно, начинается поиск всех комбинации, начинающихся с 2. Передвигаемся направо, и повторяем снова те же действия:

• Меняется 2 с 2 → 2 1 3, двигаемся направо
• Достигли последней фишки, выдать на экран 2 1 3, возвращаемся назад
• Меняется 2 с 3 → 2 3 1, двигаемся направо
• Последняя фишка - на экран 2 1 3, возвращаемся назад
• Меняем обратно 2 и 3, чтобы получилось 2 1 3, и так как сдвиг направо дает последнюю фишку, вернемся назад
• Меняется обратно 1 и 2, получая 1 2 3

Итак, вторая итерация дает на экран 2 1 3 и 2 3 1, что совершенно логично.
Точно так же работает и 3-я итерация: меняется 1 и 3, получая 3 2 1 и начинается рекурсивный спуск, который выдает на экран 3 2 1 и 3 1 2.
Алгоритм заключается в том, чтобы переставить сначала все фишки от той позиции со всеми остальными, зайдя рекурсивно к следующему элементу.

§ Общее количество перестановок

Есть один интересный факт, что количество перестановок будет равняться факториалу от числа фишек n, то есть количество = . Это легко показать. Допустим у нас есть 5 фишек. Это значит, что последовательность будет начинаться с 1-й, 2-й, 3-й, 4-й и 5-й фишки. Когда последовательность начинается с фишки 1, то это значит, что там остаются 4 фишки, и они тоже будут начинаться с 2,3,4,5. Заходя рекурсивно в каждый новый уровень, количество начинающихся фишек будет 5, потом 4, потом 3, потом 2, и потом 1.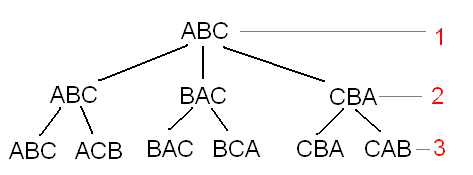

То есть, 5 раз будет использована последовательность из 4 фишек (5 * 4). В свою очередь, 4 раза будет использована последовательность из 3 фишек = 5*(4*3), и так далее, пока не будет достигнут конец. А это представляет собой факториал.

§ Программный код

1CONST n = 4
2DIM SHARED Arr(n) AS INTEGER
3
4' Инициализация массива
5FOR i = 1 TO n: Arr(i) = i: NEXT
6
7' Запуск итерации
8comb 1, n
9
10SUB comb (a, n)
11
12  ' Это последний элемент
13  IF a = n THEN
14    FOR i = 1 TO n: PRINT Arr(i); : NEXT: PRINT
15  ELSE
16    ' Обмен текущей и последующих
17    FOR i = a TO n
18
19      SWAP Arr(a), Arr(i)
20      comb a + 1, n
21      SWAP Arr(a), Arr(i)
22
23    NEXT
24  END IF
25
26END SUB