11:58
Быстрая сортировка — Лисья нора
§ Задача сортировки
Это один из самых быстрых алгоритмов, у которого, как и у всех алгоритмов, есть свои достоинства и недостатки. Сегодня я хочу разобраться в том, как он работает и расскажу об этом. Как обычно, начну с описания задачи сортировки. А задача такая: дан массив, его надо отсортировать так, чтобы элементы слева были меньше или равны элементам справа, либо наоборот, больше или равны. Другими словами, массив либо возрастает, либо убывает.Отсортировать массив можно разными способами, и этих способов достаточного много. Самая простая и наглядная из них, это, конечно, сортировка пузырьком (bubblesort), самая сложная в понимании - сортировка пирамидой (heapsort). Быстрая сортировка (quicksort) - это наиболее эффективная сортировка классическим способом перестановок элементов, но имеет такой недостаток - для нее требуется дополнительная память на стеке, поскольку сортировка рекурсивная и наихудший случай тратит много памяти и сортируется очень медленно.
Далее будем считать, что у нас есть исходный массив, назовем его
Arr. В массиве будет содержаться N элементов. Чтобы указать на самый первый элемент массива, буду обозначать так: Arr[0], чтобы указать на какой-то произвольный элемент массива, можно обозначать так Arr[i], где i - номер элемента. Если массив состоит из N элементов, то последний элемент будет Arr[N-1], потому что нумерация у нас идет с 0 до N-1.| i | 0 | 1 | ... | N-1 |
|---|---|---|---|---|
| Arr | Arr[0] | Arr[1] | ... | Arr[N-1] |
N элементов.§ Суть метода
На самом деле, метод очень простой, но требует некоторого понимания. Для начала попробуем самое простое. Допустим у нас есть некий неотсортированный массив, который надо отсортировать. Также допустим, что первый элемент массива, который надо сортировать, находится в0, а последний находится в N-1. Для примера возьмем массив из 8 элементов:i | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 Индекс ----+---+---+---+---+---+---+---+--- Arr | 6 | 2 | 9 | 5 | 3 | 7 | 8 | 1 ЗначенияОсновная идея - это сделать так, чтобы массив был поделен на 2 части (да, на 2 части). В левой части массива будут значения меньше, чем определенное число
pivot (его скажу как брать), а справа - больше числа pivot.Когда сортируется массив с помощью быстрой сортировки, число
pivot - это случайно выбранное число из массива, который сортируется. То есть, натурально, берем тупо любой индекс (обычно берут середину, но это не имеет никакого значения). Но, честно говоря, рационально брать не середину, а среднее значение, но это уже тонкости, которые пока знать необязательно.Давайте тоже возьмем середину. Середина массива находится в индексе, допустим, i=3. А что там в этом индексе? Там число 5. То есть, другими словами
Arr[3] = 5.Теперь же вокруг этого числа
pivot = 5 и будет выполняться сортировка. Алгоритм сделает так - слева будут числа, меньшие 5, а справа - большие или равные 5.§ Сортировка
Установим 2 указателяL и R. Указатель L будет указывать на самый левый край массива, а указатель R будет указывать на самый правый край, то есть L=0, а R=7. Теперь остается разделить на 2 части.Теперь идем по шагам.
L=0, Arr[L] = Arr[0] = 6 -- Arr[L] > pivot (т.е. 6 > 5), никуда не двигаемся R=7, Arr[R] = Arr[7] = 1 -- Arr[R] < pivot (т.е. 1 < 5), никуда не двигаемсяТут получилась следующая ситуация: слева значение больше чем
pivot, то есть не имеем права пропускать этот элемент, потому что надо его с кем-то обменять справа, и не просто обменять, а найти такой, чтобы он был меньше, чем pivot. И как раз такой справа и есть. Поскольку он равен 1, а 1 < 5, то надо как раз обменять 0 и 7 позицию, чтобы справедливость восстановилась. Обмениваем 0 и 7 элемент, получается следующее:
i | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 Индекс
----+---+---+---+---+---+---+---+---
Arr | 1 | 2 | 9 | 5 | 3 | 7 | 8 | 6 Значения
^ ^Поскольку обмен был совершен и слева теперь меньше, чем справа, то сдвигаем L направо, а R налево - они идут друг навстречу другу. Почему делается именно так? Просто потому, что так быстрее работать алгоритм будет. Если будет только один сдвиг (например либо справа, либо слева), то ничем это от пузырьковой сортировки отличаться не будет.Теперь
L=1, R=6. Проверим, чем равен Arr[1] = 2. Поскольку он меньше, чем 5 (pivot), то сдвигаем еще раз L=2. Проверим, Arr[2] = 9. Остановимся - потому что 9 более 5, а это не дело, нужно поискать справа какое-нибудь число, которое будет меньше 5. Ищем его.Шаг второй. Проверим
R=6, Arr[6] = 8, а 8 больше чем 5, то есть, надо дальше проверить сдвиг. Сдвигаем R=5, там Arr[5] = 7, снова больше 5, проверяем дальше: R = 4, Arr[4] = 3. Все! Нашли, наконец-то. Число 3 меньше 5 (pivot), и потому надо его обменять с левым краем.Посмотрим на то, где находятся указатели
i | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 Индекс
----+---+---+---+---+---+---+---+---
Arr | 1 | 2 | 9 | 5 | 3 | 7 | 8 | 6 Значения
^ ^Получилось так, что 1) найдено слева число, большее чем pivot, 2) справа найдено число, меньшее чем pivot. Обмениваем их! И после обмена сразу же сдвигаем указатели друг к другу. Левый сдвигается на +1, правый на -1.
i | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 Индекс
----+---+---+---+---+---+---+---+---
Arr | 1 | 2 | 3 | 5 | 9 | 7 | 8 | 6 Значения
^Получилась та ситуация, что указатели L = R, они стали равны. Так получается не всегда, но это типичная ситуация. Это не повод останавливать алгоритм. Это означает, что мы должны двигаться до тех пор, пока R не станет меньше, чем L. Это очень важный момент.Давайте пока взглянем на то, что получилось. Оба указателя по счастливой случайности остановились в индексе
i=3, и мы видим, что тут как раз и находится pivot. Также видно, что все элементы слева меньше чем 5, а все элементы справа - больше чем 5. Не стоит переживать, что они находятся в разбросанном порядке, хотя с левой стороны вообще все отсортировано как надо. Справа же массив все еще не отсортирован.Далее. Поскольку алгоритм все еще не остановился, надо сделать следующее: передвинуть снова L на одну позицию направо, а R - налево, т.е. они примут значения
L=4, R=2. Поскольку L > R, выходим из цикла сортировки.
i | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 Индекс
----+---+---+---+---+---+---+---+---
Arr | 1 | 2 | 3 | 5 | 9 | 7 | 8 | 6 Значения
R LВидим, что R указывает на правый край левого массива (элементы 0, 1, 2), а L указывает на левый край правого массива (элементы 4, 5, 6, 7). Что это значит? Это значит только одно - эти массивы как раз и надо сортировать снова. То есть делаем следующее: выполняем ту же самую сортировку для массива [0..2], и ту же сортировку для массива [4..7]. Это и есть тот волшебный рекурсивный спуск.По итогу, получается, что QuickSort делает следующее: делит массив на 2 части, где элементы одной части меньше элементов второй (гарантированно), а потом тем же способом сортирует эти 2 части и так до тех пор, пока не дойдет до того момента, когда будет разница между L и R равна 0, и сортировать будет нечего.
§ Программный код
Ниже приведена программа, написанная на Quick Basic 4.5, для демонстрации сортировки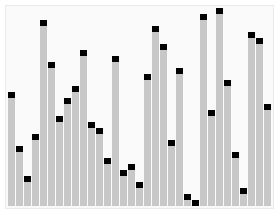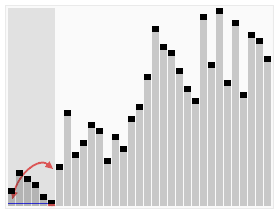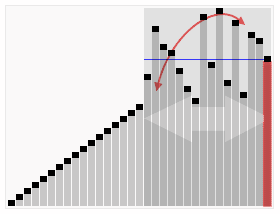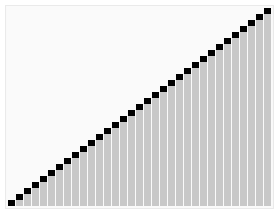
SUB QSort(l%, r%) a% = l% b% = r% pivot = Arr((l% + r%) \ 2) DO ' Поиск левого и правого края для обмена значениями WHILE (Arr(a%) < pivot): a% = a% + 1: WEND WHILE (Arr(b%) > pivot): b% = b% - 1: WEND ' Обмен со сдвигом к центру IF a% <= b% THEN SWAP Arr(a%), Arr(b%) a% = a% + 1 b% = b% - 1 END IF LOOP WHILE a% <= b% ' Если есть подмассивы для сортировки IF l% < b% THEN QSort l%, b% IF a% < r% THEN QSort a%, r% END SUB