§ Линейная функция
Обычный перцептрон состоит из двух частей: сумма весов и активационная функция. Активационная функция может быть разной, но сумма весов, как правило, всегда одинакова и выглядит так:В данном случае является весовым коэффициентом, а — входящим параметром, передаточным сигналом, входом, и т.п. Обученная нейронная сеть не меняет без необходимости (кроме случаев дообучения, возможно даже, на лету).
Теперь я разберу некоторый случай. Начну немного издалека, представив миру следующее уравнение:
Что из себя представляет это уравнение? Оно представляет из себя некоторую линию под наклоном . Что из себя представляет ? Представим, что =1, получим , линию, проходящую под 45 градусов. Дело в том, что — это тангенс угла, это значит, что:
Где параметр
b — перпендикуляр к оси X (или отрезок по Y), и a — перпендикуляр к оси Y (или отрезок по X). Это значит, что линию можно представить в виде; ;
Стоит учесть тот факт, что подобная линия будет проходить через (0,0). Чтобы линия проходила через некоторую произвольную точку по оси Y, то надо добавить свободный коэффициент C, например:Как видно, чтобы задать уравнение линии в общем виде, нужен вектор , который является нормалью (повернут на 90 градусов).
Как можно заметить, если заменить уравнение прямой на другие параметры, например, и поменять на , , аналогично сделать с , :
Получится весовая функция. Так что на самом деле представляет из себя ядро нейрона? Дело в том, что линейная функция — это общее уравнение прямой или n-мерной плоскости, например. Весами выступают здесь параметры к этой плоскости. Сами по себе веса это вектор нормали к плоскости. Но это знание сейчас совершенно ни о чем не говорит.
§ Прямая линия
Чтобы разобраться лучше в сухой теории, всегда лучше показать несколько примеров. Начнем с простого:y = x, где a = 1.
Легко заметить линию, проходящую под углом 45 градусов. Уравнение этой прямой известно:
-
y - x = 0(x перенесен из правой части) -
x - y = 0(y перенесен из левой)
Теперь есть одна интересная деталь. Мы можем всегда сказать, с какой именно стороны такой линии находится произвольная точка A(x,y). Как это это узнать?
Из уравнения
y = x видно, что любая точка, которая бы находилась выше или левее чем y, будет, собственно говоря, выше чем y, как бы это парадоксально ни звучало. То есть y + C > y, если C > 0.Так оно и есть, если вычесть из этого уравнения оба
y, то останется C > 0.Представим же так:
Но дело в том, что у нас
y = x, поэтому:То есть, заменяем правый
y на x (поскольку они полностью равнозначны). Теперь, переносим x налево:И что получается? Получается, что если
C больше 0, то уравнение будет тоже больше 0, а значит, точка находится слева. Аналогично, если результат уравнения будет меньше чем 0, то точка находится справа.
Вот теперь можно взглянуть на результат. Там где
C оказался положительным, нарисовано зеленым цветом, там же где отрицательным — синим.§ Косая линия
Как обычно, ничего не понятно из объяснений, поэтому приведу еще несколько примеров. Так выглядит график функцииy = 2x.
Легко заметить из графика, как с каждым x+1 прибавляется y+2, и если подумать, можно взять любые две точки и провести через них произвольную прямую. Вот пример, взять вектор (3,2) и провести прямую через (0,0):
или или
Как я и рассказывал ранее, чтобы получить общее уравнение произвольной прямой, достаточно лишь получить только вектор.

Как видно, через каждые +3 точки по X увеличивается на +2 по Y. Любопытный факт в том, что к коэффициентам получается вектор (2,-3). Если провести его через точку (0,0), то получится прямая, которая будет перпендикулярна к исходной прямой. Этому есть объяснение, но я вдаваться в подробности не буду, поскольку в данной статье это не имеет значения.
Уравнение линии равно 0 в том, и только в том случае, когда (x,y) лежат на этой прямой. В этом и есть смысл именно уравнения линии. Но что будет, если точки не будут лежать на прямой? Это означает, что итоговое уравнение будет не равно 0, и будет либо больше 0, либо же меньше. Для нейросетей это играет ключевую роль.
Нейросети — это прежде всего, задачи классификации, распознавания, или даже предсказания на основе предыдущих результатов. Казалось бы, причем тут линейные функции? Что они делают и зачем?
§ Определение сторон
Давайте представим очень простую ситуацию, которую может выполнить нейросеть. Существуют N точек на плоскости, причем они разбросаны так, что часть точек находится с одной стороны, а часть точек — с другой. Задача нейросети разобраться и найти алгоритм, по которому бы точки можно было бы разграничить между собой, классифицировать.
С одной стороны находятся 3 красных точки, а с другой 2 синих. Задача в том, чтобы найти линию, которая бы разделила область наполовину, отделив красные и синие точки, то есть, по сути, необходимо найти a,b,c:
Выше представлено общее уравнение прямой. Его также можно преобразовать в такой вид:
Но на самом деле, в таком виде мы представляем лишь для наглядности с 2х мерным пространством. Для 3х мерного пространства такой вид уравнения будет уже неудобен и лишь создаст дополнительные проблемы с пониманием.
Нейросеть с помощью метода обратного распространения ошибок с легкостью найдет решение этого случая, поскольку он очень прост. То, как работает этот метод, будет рассказано в будущем, но примем за факт, что решением будет являться линия с параметрами a=-1, b=1, c=0 или просто

Если принять за функцию результат вычисления
f(x) = -1*x + 1*y + 0, то при положительном f(x) все заданные точки красного цвета (на втором графике — желтого) будут находиться слева, или при положительном значении, допустим, это будет 1, а все точки, которые находятся слева, будут принимать значение отрицательное, то есть 0.Простейшая задача классификации решена. Но это лишь самая простая из всех возможных задач. Реальные же нейросети способны распознавать абсолютно все что угодно: главное, выбрать правильную архитектуру сети и обучить.
Это и есть первая задача нейросетей.
§ Многомерное пространство
Естественно, мы не будем делать нейросети и нейроны, у которых будут только 2 входа, потому что это слишком простые сети и они ничего не смогут решить. Входов может быть сколько угодно, но каждый нейрон, в силу особенностей своей функции, занимается только одним делом — он разделяет пространство на 2 части.Если у нейрона 3 входа, то с точки зрения геометрии, он представляет из себя 3-х мерную плоскость, которая разделяет трехмерное пространство на две части — либо с одной стороны (например, слева от плоскости) будут положительные значения, либо с другой стороны — отрицательные. При попадании точки на саму плоскость результат будет 0, что следует из самого уравнения плоскости.
Если у нейрона 4 и более входов, то происходит деление пространства на 2 части все равно — на левую и правую сторону, но пространство будет уже на 3-х мерных, а многомерным. В любом случае, представление нейрона как геометрического объекта, конечно же, бессмысленно, но для наглядного понимания следует помнить, что нейрон занимается задачей классификации очень и очень простой: он всего лишь делить надвое пространство.
Это значит, что при задании некоторых входов нейрон может сказать — положительно или отрицательно значение, а также то, насколько далеко указанная точка находится от плоскости (но не совсем точно, это лишь оценочное число). Выходит так, что нейрон, своего рода, выполняет оператор условного ветвления (IF). Несмотря на это, нейросети умеют считать, как минимум, их можно научить абсолютно всему, поскольку выполняя деление пространства на две части, нейросеть способна научиться любому линейному алгоритму, так как содержит в себе условия условного ветвления.
§ Моделирование булевой алгебры
Допустим, если взять булеву алгебру, то нейросеть способна на то, чтобы используя входы A, B в качестве аргументов, выдать результат любой булевой функции, например NAND, NOT, AND, XOR и другие. Так как любую комбинаторную функцию можно свести к одному лишь NAND, то научить нейросеть распознавать такую операцию не составит никакого труда.По идее, для того, чтобы выдавать результат NAND, нейросеть достаточно обучить следующим 4 случаям:
A B = R -1 -1 | 1 -1 1 | 1 1 -1 | 1 1 1 | -1То есть, при A=1, B=1 будет R=0, иначе 1. Если представить на графике эти 4 точки, то они будут выглядеть так:


Чтобы получить такой результат, потребуется лишь 1 линия на двухмерной плоскости, и она показана на рисунке. Линия проходит не через центр координат (0,0), а смещена слегка выше:
Коэффициенты (веса) нейросети будут равны . Кстати, третий вес нейрона — это всегда свободный член, предполагается, что на вход всегда подается 1. Это необходимо для того, чтобы линия была представлена наиболее точно.
Можно попробовать убедиться в том, что коэффициенты к уравнению подобраны верно.
- Возьмем x=-1, y=-1, проверим 1-(-1)-(-1)=1+2=3, результат положительный, значит, 1
- Возьмем x=+1, y=-1, проверим 1-(+1)-(-1)=0+1=1, результат положительный, значит, 1
- Возьмем x=-1, y=+1, проверим 1-(-1)-(+1)=2-1=1, результат положительный, значит, 1
- Возьмем x=+1, y=+1, проверим 1-(+1)-(+1)=1-2=-1, результат отрицательный, значит, -1
Это не значит, что нейросети надо обучить выполнять функции процессора (хоть это и возможно). Это лишь говорит о том, что они способны на любую комбинаторную функцию, и только. Если это так, и если добавить узлы запоминания, или возможность рекуррентности, то есть, когда сигнал распространяется не вперед только, но и назад, в том числе, то возможно создать процессор любой сложности, машину, полной по Тьюрингу.
§ Сигмоида
После того, как более-менее понятно, что делает линейная функция в искуственном нейроне, остается еще один вопрос — функция активации, сигмоида, или вообще, любая другая.Простейшая функция активации — это функция, которая выдает -1, если результат отрицательный, или +1, когда положительный. По идее, именно этой функцией активации (ступенчатая) мы и пользовались параграфом выше. Сигмоида выполняет почти ту же самую функцию, что и бинарная, но она намного более сглаженная посередине, и выдает не от -1 до 1, а от 0 до 1. Функция сигмоиды равна 0.5 при аргументе, равном 0.
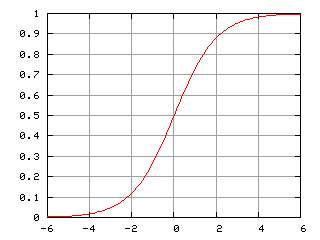
Почему именно сигмоида? Это достаточно простая функция для того, чтобы использовать ее для поиска антиградиента, о нем позже речь, но в то же время, она и достаточно медленная, поскольку требуется не просто деление, но и вычисление экспоненты. С какой-то стороны, эта функция достаточно быстрая, для выполнения метода обратного распространения ошибки, но медленная для прямого вычисления, когда требуется получить результат.
Существует гораздо более быстрая функция активации, ReLU. Она крайне проста, и ее функция легко вычисляется:
-
x <= 0, y = 0 -
x > 0, y = x