Главная » Математика » Теорема косинусов

§ Трям

Сейчас речь пойдет про теорему косинусов, которая будет невероятно важна для того, чтобы понимать все остальные теоремы. Доказывать, доказывать, и еще раз доказывать свою правоту! Вот что говорил Пифагор, но это не точно.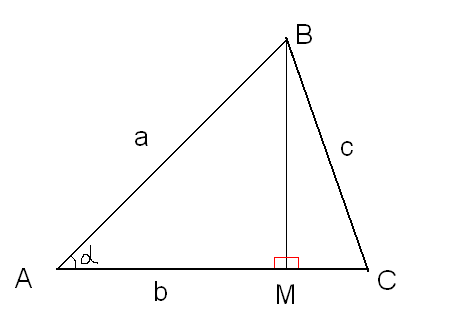

Рассмотрим треугольник. Он красивый, не правда ли? Единственно, что только эта альфа ни к селу ни к городу, как будто, но не все так просто. Много воды не бывает. А если много воды, то это уже океанический штормовой. Так вспомним же! Что такое косинус?
Косинусом называется: прилежащий катет поделен на гипотенузу (какой-то мудрец)
Найдем лупу и начнем искать катет и гипотенузу (не гиппопотама). Итак, таким катетом оказался отрезок AM, а гипотенуза расположена в AB.

§ Мегавывод

То есть, cos(a) = \frac{AM}{AB} = \frac{AM}{a} => AM = acos(\alpha) , таковы дела. Займемся воспоминаниями о Теореме Пифагора, которая гласит, что:
AM^2 + BM^2 = a^2
MC^2 + BM^2 = c^2
Либо можно приравнять их:
BM^2 = a^2 - AM^2
BM^2 = c^2 - MC^2
Получаем:
c^2 - MC^2 = a^2 - AM^2
c^2 - a^2 = MC^2 - AM^2
Теперь заменим AM = acos(\alpha) , MC = b - acos(\alpha)
c^2 - a^2 = (b - acos(\alpha))^2 - (acos(\alpha))^2
c^2 - a^2 = b^2 - 2abcos(\alpha) + (acos(\alpha))^2 - (acos(\alpha))^2
c^2 - a^2 = b^2 - 2abcos(\alpha)
c^2 = b^2 + a^2 - 2abcos(\alpha)

§ Конец

Мы только что обыкновенно доказали, что ничего недоказанного в мире теорем косинусов нет, и что она выглядит так:
c^2 = a^2 + b^2 - 2abcos(\alpha)
Отсюда идут далекоидущие выводы, что можно рассчитать косинус, зная все стороны треугольника, не обязательно он должен быть прямоугольный.
c^2 - a^2 - b^2 = -2abcos(\alpha)
a^2 + b^2 - c^2 = 2abcos(\alpha)
cos(\alpha) = \frac{a^2 + b^2 - c^2}{2ab}
12 мая, 2020
© 2007-2024 Мощные леса бегут