§ Отказ от ответственности

У меня лучше, чем в учебнике, все равно не получится рассказать, к тому же на Википедии есть подробный и понятный разбор. Но я эту статью пишу потому что у меня графомания. И моя цель в том, чтобы просто так написать еще одну ненужную статью.

§ Нулевой рост

Итак, производная функции - это скорость изменения в какой-то ее определенной точке. Вот и всё определение производной, на самом деле.
Я рассмотрю несколько примеров. Пример первый (и последний):
Да, это функция, которая значит, что y равен 5 всегда, независимо от того, какой будет вообще x. Вместо 5 может быть вообще любое число (даже комплексное, не имеет значения). Далее можно говорить, что где будет число, там можно заменять символ C - в переводе с русского на английский — это константа, какое-то неизменяемое произвольно число вообще. То есть реально, какое хочешь число бери и обозначай как C (переводится как Constant). А вот и график этой функции: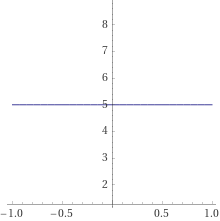

Как можно заметить, тут происходит нечто интересное, а именно: ничего не происходит. Просто линия. Если подумать здраво и логически, то с какой скоростью возрастает такая линия? Ответ очень простой — ни с какой не возрастает. У любой линии, будь то 5, или -100500 или даже более 9000 - скорость роста никакой, и поэтому карьера у нее не задалась. А это значит, раз мы называем производную скоростью роста, то производная от константы будет всегда равна нулю (или 0).

§ Начинаем карьерный рост

Поскольку у предыдущий функции рост 0, надо найти такую, у которой был бы рост. И такая найдется:
Интересно, правда ли? Теперь я на графике покажу, что происходит с этой функцией:

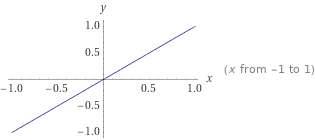
Как видно из графика, функция, действительно, постоянно куда-то растет вверх (причем бесконечно) - если смотреть слева направо, конечно, но тут надо быть оптимистом. Тем пессимистам, кто смотрит справа налево, кажется, что функция убывает, но не суть.
Ладно, давайте перейдем к делу и проверим, так куда же она растет и как. Допустим, надо посмотреть, с какой скоростью происходит рост в точке, допустим 7. Как это измерить? Что такое вообще скорость роста?
Скорость — это некое изменение показателя во времени. За время берем x (аргумент функции называется), а за показатель возьмем значение функции y(x). Пример берем прямо вообще простой: у Вовочки было 5 яблок, а через 1 минуту стало 6. Через одну минуту стало 7, через минуту стало 8. Какой вывод из этого? Вывод такой, что каждую минуту у Вовочки с неба падают какие-то яблоки (1 штука в 1 минуту). О чем это может говорить? Что Вовочка — яблочный магнат. Ну и то, что у него 1 яблоко в минуту добавляется. Скорость роста - 1 яблоко в минуту.
А что делать, когда мы знаем что у Вовочки было 1 яблоко, а потом стало 5 яблок через 4 минуты? Какая будет скорость роста? Хм, тогда надо будет взять разницу в количестве яблок и поделить на разницу во времени, так?

• Разница в количестве яблок: было 1 — стало 5, разница — 5 минус 1 = 4
• Разница во времени: 4 минуты, потому что мы так и сказали — через 4 минуты, значит, разность времени 4 минуты.

И что получается? Скорость роста яблок у Вовочки такая - 5 минус 1 равно 4, и эту 4 делим на 4. Получаем что опять, 1 яблоко в 1 минуту:
Но математика штука абстрактная. Теперь вместо чисел я подставлю неизвестные какие-нибудь. Допустим, у Маши было конфет (количество конфет). Через некоторое время у Маши стало конфет. С какой скоростью Маша поедает конфеты? Тут появился новый символ - он лишь означает разность. Допустим говорит о разности между конечным значением N и начальным значением N (допустим, количестве конфет у Маши). Например, было 5 конфет (начальное N) и стало 10 конфет (конечное N), значит = 10 - 5 = 5.
Средняя скорость роста конфет у Маши (в минутах). Именно средняя скорость роста! Не та скорость роста в конкретный момент, а средняя!
Тем самым, подставляя значения a, b и можно рассчитать среднюю скорость роста.
Теперь же перейдем к функции, которая выше была. Вместо a и b надо подставить значения функции при неких определенных x. Давайте пробовать:

• Рассчитаем какой будет y при x=0; он там будет равен y=0
• Рассчитаем какой будет y при x=1; он будет равен y=1

Хорошо, какая тогда средняя скорость роста? Тут все очевидно - скорость роста будет 1. Почему? Потому что если из 1 вычесть 0 и разделить на 1, будет 1. Ладно. Берем другие значения:

• x=5, вычисляем y и он будет равен 5
• x=7, вычисляем y=7

Вычитаем 7 минус 5 = 2. Хорошо, а что дальше? Вычитаем теперь по иксу 7-5 и будет равно 2, делим 2 на 2 и получается, что опять 1!
Да почему же всегда будет одно и то же число 1? Давайте представим теперь более общую формулу вычисления любой скорости изменения:
То есть смотрим, что тут происходит. Дельта x (то есть ) — это тот отрезок (к примеру, времени), за который надо вычислить прирост функции, а выражение сверху - это значение, которое получается после прибавления этого интервала и вычитания из первоначального значения.
Пример: возьмем = 1 (от балды конечно же). Возьмем функцию . Надо вычислить скорость роста функции в точке x=6.

• Вычисляем y(6) = x = 6
• Вычисляем y(6 + ) = y(6 + 1) = y(7) = 7
• Вычитаем y(6 + ) - y(6) = 7 - 6, получаем 1
• Делим на — 1 делится на 1, получается 1

И чтобы мы не делали, всегда получается 1 и все тут. Ладно. А что если взять другую дельта? Например = 0.1? Вычислим, например, скорость роста функции в точке x=2.

• Вычисляем y(2) = 2
• Теперь вычисляется значение функции в точке 2 + 0.1 (дельту добавили): y(2 + ) = y(2 + 0.1) = 2.01
• Вычитаем y(2.01) - y(2) = 0.01
• Делим на ... 0.01 делим на 0.01 и опять 1!

Вот это поворот!
Другими словами, какой бы x или дельту x не брали бы, всегда и везде скорость роста равна 1. То есть, можно сказать так, что:

Производная по x функции y(x)=x будет равна 1

Ненуачо, удобно. Еще производную можно записать в таком виде: . То есть, например, производная
А ведь я еще про лимиты ничего не говорил, а уже производную взяли.

§ Лимиты...

Хорошо, вот научились вычислять среднюю скорость в некоторой конкретной точке. Но средняя скорость — это все-таки, средняя скорость роста, а этого мало, надо узнать, какая же будет точная скорость. Предыдущий пример показал, что для монотонно возрастающей линии средняя скорость вообще везде одинаковая, с какого бока не возьмешь, но ведь функции не только линии бывают, всякие бывают, там уже среднюю скорость не так просто взять.
А как быть? На самом деле, все очень просто. Надо лишь постепенно уменьшать . Чем меньше это значение, тем точнее будет результат. Почему так? Это из-за того, что если мы будем брать = 1, то за то время, пока пройдет минута (или час, год, галактический год, время от рождения до конца Вселенной - это тоже может быть единицей всё), произойдут много событий. Тогда, чтобы поточнее вычислить, и приходится уменьшать интервал проверки.
Взглянем на формулу:
Здесь видно, что мы добавляем дельту к иксу, вычисляем то значение функции, которое там будет, вычитаем из значения функции, которое сейчас есть и делим на эту дельту — получаем некоторую среднюю скорость, которая была за этот интервал дельта икс.
И тут происходит магия! ВЖУХ!! И дельта икс начинает все становиться меньше и меньше, меньше и меньше, меньше и меньше, меньше и меньше и такой микроскопической, что в электронный микроскоп уже не разглядишь. Но как бы тут не было! Оно уменьшается и дальше, дальше, дальше... бесконечно уменьшается и уменьшается. И никак уменьшиться не может. Так мы и прождем бесконечное количество времени, пока оно не уменьшится. И знаете что? Оно никогда не уменьшиться до 0. Оно всегда будет в процессе уменьшения.
Это называется лимит. То есть, такое число, которое всегда к чему-то стремиться, ни никогда его не достигнет. Бывает, что стремится это число к 0, бывает - к бесконечности (в минус бесконечность или в плюс).
Вот теперь производная записывается правильно. В этой формуле изображено вычисление некоторой средней скорости при дельта x (), который постоянно стремится к 0, а значит, средняя скорость постоянно стремиться стать точной скоростью.
И что дальше? Как применить это на практике? Давайте теперь попробуем вычислить точную скорость y(x)=x, но теперь — с помощью лимитов.
Итак, поскольку y(x)=x, то это несложно. Просто подменяем везде y(x) на x:
Видно, что если вычесть x минус x, то будет 0, значит, останется вот что:
Как можно заметить, значение числа тут вообще никакой роли не играет.

§ Еще один пример

Давайте еще какую-нибудь функцию проверим? Например , где число a - это какое-то заданное заранее число, любое, например 5 или -3 или вообще какое угодно число.
Оно рассчитывается совершенно аналогично:
То есть, тут тоже значение никак не повлияет, а в итоге получится число a. Это говорит о том, что производная от функции будет равна , то есть так: .

§ Производная от квадрата x

Существует такая функция, как . Она хорошо всем знакома и выглядит на графике вот таким образом: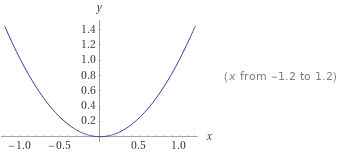

Если присмотреться, то она вообще не выглядит как прямая линия. Это означает только то, что в разных местах она растет с разной скоростью. Но с какой именно? Например, в точке x=0 она не растет, там скорость роста 0. Я не имею ввиду среднюю скорость роста, а конкретно скорость роста функции в точке 0.
Если чуть отодвинуться вправо, то скорость роста будет положительной (снизу вверх), и все время возрастать. Это значит, что скорость роста функции тем быстрее, чем дальше вправо по x. Соответственно, скорость падения будет слева от x=0, то есть, в отрицательных значениях будет падения, в при положительном x>0 будет рост.
А какой именно? Как это рассчитать?
Вот как раз для этой цели и нужна производная. Если мы получим производную от функции, то всегда и в любой момент можно узнать скорость роста и падения в точке (причем бывает, что и не бывает точки, где можно сказать, какая там скорость роста).
Итак, чему будет равна производная? Для этого, вставим необходимую нам функцию в ту самую общую формулу для вычисления производных:
Нужно раскрыть скобки у выражения =
С учетом этого, подставляем в формулу выше:
Хорошо видно, что сокращаются, потому что один вычитается из другого. Теперь остается разобраться, что по итогу выйдет. Надо поделить все на :
А вот теперь видим, что дельта тут фигурирует. Но, если вспомнить, что она постоянно стремится к 0, то допускается то, что где-то в бесконечном конце оно так и станет этим 0. Потому вместо ставим в выражение 0, убираем лимит и получается следующее:
Вот это да! Сейчас доподлинно известно, какая будет скорость роста для любой точки на функции. Теперь можно много чего рассчитать таким же самым методом, но я в этой статье этим заниматься не буду.

§ Касательно касательной

Ранее было рассмотрено выше, что производная это отношение прироста функции к приросту ее аргумента . Конечно же, тут уменьшается и приближается к 0 постоянно.
Рассмотрим рисунок:

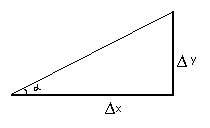
На рисунке как раз виден дельта Y и дельта X. Существует такая тригонометрическая функция, как тангенс, который равен отношению противолежащего катета в прямоугольном треугольнике к прилежащему катету . Это означает, что производная в точности равна тангенсу!
И что это означает? То что раз производная - это тангенс, то, во-первых, можно найти угол (хотя это не особо важно), и по этому углу — уже найти касательную к точке. А что такое касательная? Это некая прямая, которая проходит через одну точку функции и строго параллельна этой точке.
Поэтому, геометрический смысл производной — в том, что это является касательной, можно построить прямую касательной.