Главная » Математика » Что интереснее -- интеграл или тригонометрия?

§ Есть два способа

Всегда есть два способа вычислить площадь — либо с помощью линейки и ручки, или с помощью интеграла. Сегодня я просто для прикола расскажу о некотором способе вычислить интегралом или геометрией.

§ Площадь прямоугольника

Интегралом можно подсчитать не только площадь некоторой функции, но также и площадь прямоугольника. Понятное дело, что это легче легкого, но ведь надо с чего-то начать объяснения.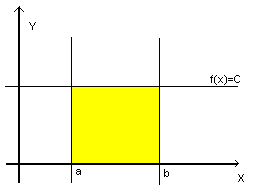
ab1.png
Задана функция f(x) = C , где C — некоторое определенное, любое число, ну, пусть будет C = 10. Прямоугольник начинается в точке a и заканчивается в точке b по оси X. Одна сторона прямоугольника равна 10 (это высота прямоугольника), а вторая сторона равна b - a , допустим, что b=20 , a=5 , тогда 20-5=15 . Другими словами:
S = C(b-a) = 10 \cdot 15 = 150
Это в нашем случае с прямоугольником.

§ Определенный интеграл

Задача определенного интеграла — подсчитать площадь функции на диапазоне от [a, b] . И всё. Интеграл также подсчитывает и отрицательные площади, как ни странно. Если функция выйдет в минус, то такая площадь будет считаться как отрицательная. Достаточно лишь привести вот такую форму:
\int_{a}^{b} f(x) dx = F(b) - F(a)
Здесь F(b) и F(a) это первообразные, обратные функции к интегралу. Пример, если первообразная F(x) = x^2 , то тогда если мы ее продифференцируем, то F'(x) = 2x . Говоря так, первообразной от 2x будет x^2 + C .
Подсчитаем площадь прямоугольника через интеграл:
S = \int_{a}^{b} C dx = Cb - Ca = C(b-a)
Что полностью совпадает с функцией выше, кстати.

§ Площадь функции, заданной прямой

Как известно, прямая может задаваться вот таким вот образом:
y = Ax + B
Тут A,B — некоторое коэффициенты. Теперь надо попробовать пересчитать ее через классический геометрический метод и с помощью интеграла и посмотреть, что из этого будет попроще. Спойлер: интеграл здесь будет проще.
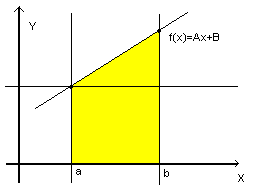
ab2.png
Рассмотрим рисунок. Фигура состоит из двух частей:
  • Прямоугольника
  • Треугольника
При сложении этих двух частей получится общая площадь. Теперь попробуем подсчитать. Нижний прямоугольник имеет высоту y = A \cdot a + B , где вместо x значение a . Ширина этого треугольника равна разности b-a . Итого, площадь прямоугольника равна, что вполне очевидно.
S_1 = (Aa + B)(b - a) = b(Aa + B) - a(Aa + B) = A \cdot ab - Aa^2 + Bb - Ba = Aab - Aa^2 + B(b - a)
Теперь же подсчитаем площадь треугольника. Одна сторона его будет известна и равна b-a , вторая же сторона представляет собой разность:
y(b)-y(a)=Ab + B - (Aa + B) = A(b-a)
Площадь треугольника поэтому равна:
S_2 = \frac{A(b-a)(b-a)}{2} = \frac{A}{2}(b-a)^2 = \frac{A}{2}(b^2-2ab+a^2) = \frac{A}{2}(b^2+a^2)-Aab
Объединим две площади в одну:
S = S_1 + S_2 = Aab - Aa^2 + B(b - a) + \frac{A}{2}(b^2+a^2)-Aab = B(b - a) - Aa^2 + \frac{A}{2}(b^2+a^2)
Остались последние штрихи. Я домножу на 2 числитель и знаменатель:
S = B(b - a) + \frac{Ab^2}{2} + \frac{Aa^2}{2} - 2\frac{Aa^2}{2} = B(b - a) + \frac{Ab^2}{2} - 2\frac{Aa^2}{2}
Окончательный ответ:
S = \frac{A}{2}(b^2 - a^2) + B(b - a)

§ А теперь интеграл

Ну и теперь покажу, как легко и просто все это решается интегралом. Для начала, найдем первообразную для f(x) = Ax + B :
F(x) = \frac{A}{2}x^2 + Bx + C
И пользуясь формулой вычисления площади:
S = F(b) - F(a) = (\frac{A}{2}b^2 + Bb + C) - (\frac{A}{2}a^2 + Ba + C) = \frac{A}{2}(b^2 - a^2) + B(b - a)
Всё! И ведь это очень простой случай. Интегралом можно считать не только такие, линейные функции, которые можно высчитать геометрически, а любые, даже самые запутанные. Это конечно, в случае, если их получится интегрировать, найти их первообразную.
24 мая, 2024
© 2007-2024 Все коты отлично зарезервированы