Оглавление
§ Треугольники
Сегодня я хочу что-то доказать, то, что не доказывал раньше. Я учился в школе, но в одно ухо влетело, а в другое ухо тоже влетело, но потом, и красное было неделю, поэтому пифагорейца из меня не вышло, но я постараюсь, спустя, ээээ, лет 18, исправить положение дел и начать заниматься элементарной математикой в 31 год в 2019 году, 12 марта, весной.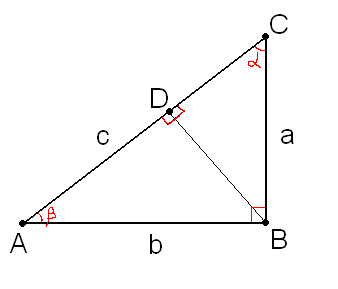
На этом рисунке, который я нарисовал в MSPaint в Windows XP в 2019 году (XXI век на дворе, товарищи), нарисован прямоугольный треугольник ABC и еще куча всяких. У треугольника есть прямой угол в 90 градусов. Сторона это BC, сторона это AB, сторона это AC. И еще заметим, что проведена высота BD к стороне AC. Высота образовала 2 прямоугольных треугольника ADB и CDB.
Теперь такое замечание. Треугольник ADB подобен треугольнику ABC, так же, как CDB подобен треугольнику ABC. Это почему еще?
На этот вопрос пришлось мне потратить огромное время. Я с трудом понял, почему так получается, но потом добрый гугл подсказал, что дело в том, что углы у ABC, CDB и ABC в 90 градусов! Это важно! Они все прямоугольные. И это еще не все!
По секрету скажу: у CAB и у DAB - углы одинаковые. Только тсс, никому! Открою секрет — эти углы у них общие. И это все решает в итоге. То есть 2 угла у треугольника одинаковые, 90 градусов у одного, и еще общий угол у другого, это значит, что эти треугольники друг другу подобны. А что такое подобны? Очень просто, это когда берешь один треугольник и увеличиваешь его в K раз или уменьшаешь, и он превращается, как по волшебству, в другой треугольник.
Возьмем 2 подобных треугольника ADB и ABC. У них подобны стороны друг другу вот эти: AD и AB, AB и AC, BD и BC. Если разделить эти стороны, то получим один и тот же коэффициент подобия.
§ Первый треугольник
Потребуется только это:Обратим внимание на то, что AB это , AC это
Умножая обе части уравнения на , получим
§ Второй треугольник
Точно тем же способом находятся соотношения между треугольником CDB и CBAПотребуется только это:
Обратим внимание на то, что BC это , AC это
Умножая обе части уравнения на , получим
§ Финальное сложение
Теперь пришло время складывать и понимать. У нас есть 2 формулы:Может их сложить? Ничего плохого не случится.
Занимательная математика!
А что такое CD + AD? Это же AC! Присмотреться если на рисунок, то там CD и AD составляют AC, но AC - это c. И что имеем
То есть:
Пифагор был великим человеком. Вечная слава ему. Ой, а вдруг сглаз будет у Пифагора? Тьфу-тьфу-тьфу, пусть уж лучше Пифагор живет и здравствует.