§ Площадь треугольника

Сегодня пойдет разговор про вычисление различного рода объемов, площадей через интегралы. Мне показалась эта тема достаточно интересной и любопытной, и я захотел ее просто так рассмотреть, хотя никакого практического смысла она не имеет.
Для начала рассмотрю классический треугольник и как подсчитать площадь через формулу вычисления площади прямоугольных треугольников

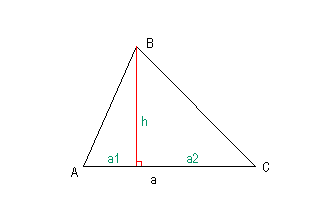
Есть высота и основание . Треугольник состоит из двух прямоугольных треугольников с катетами , и . Формула вычисления площади прямоугольного треугольника простая . Подставим нужные значения и . Сложим . Все доказано, собственно. Другим словами, получается что вычисление площади любого треугольника - это умножение его основания на высоту и деление на 2, т.е. тоже самое что вычисление площади прямоугольного треугольника.

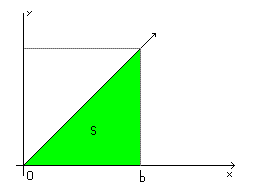
А теперь рассчитаю через интеграл. Определенный интеграл - это площадь функции от до . Поскольку считаем треугольник, то считать будет прямоугольный треугольник, как ранее и было выведено. То есть, в точке будет 0, а в точке значение должно быть (основание). Будет взят определенный интеграл . Функция, которую будем считать это . Действительно, если то , и . Условия соблюдены.
Вот и все, что надо было знать про треугольники.

§ Объем прямоугольной пирамиды

На самом деле, объем пирамиды считается точно тем же самым способом, что и считается площадь треугольника, просто изменяется функция подсчета. Для пирамиды в ее вершине, как и треугольнике, должна быть , но в основании функция должна принять вид , т.е. площадь квадрата. Но функция получается не совсем линейная. В точке функция должна описывать , т.е. получается что на самом-то деле. Значит, получается так . Но нам нужно сделать так, чтобы в было , поэтому итоговой функцией будет . Проверим. Очевидно что в будет 0. Теперь проверим, что будет при :
Все верно. Считаем интеграл:
Причем тут - это именно основание пирамиды, и оно может быть вообще любым. Так что можно переписать следующим образом и это будет правильно: