§ Вывод соотношения

Сегодня я разберу, как вывести общее уравнение для линии, заданной в 2D-пространстве по двум точкам. У такой линии есть, как я и говорил, 2 точки - начало и конец, пусть это будет точка и точка , а также потребуется точка , которая будет представлять собой неизвестные значения, которые должны лежать на прямой и удовлетворять уравнению.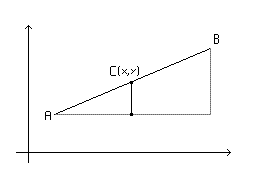

На рисунке показан прямоугольный треугольник. Здесь легко заметить, что точка лежит (и должна лежать) на линии . Эта точка образует подобный треугольник по двум углам - один общий, другой угол в 90° Итак, можно сделать такой вывод, что:
Поскольку треугольник подобен, то подобны все его стороны. Если теперь перемножить левую и правую часть на то получится следующее:
После раскрытия скобок и перегруппировки выходит следующий результат:
Нетрудно заметить, что получается каноническое уравнение прямой.
Где коэффициенты равны:

§ Нормаль

У такого вида уравнения прямой есть еще одна интересная особенность. Дело в том, что вектор, получаемый с помощью координат , перпендикулярен к основной линии. Это легко доказать, зная, что скалярное произведение векторов, между которыми прямой угол, равен 0:
Первым вектором будет выступать сама линия, вторым вектором будет выступать вектор , полученный через . Выполним скалярное произведение:
Что и требовалось доказать. Можно еще доказать методом поворота, но это уже метод немного посложнее.
Теперь же, чтобы получить нормаль, необходимо всего лишь найти длину вектора, и разделить этот вектор на свою длину: