§ Вывод формулы для отражения

После всех перипетий, наконец, можно приступить к рассмотрению такой интересной вещи, как зеркальное отражение. Я сам недавно о нем узнал, примерно недели 2 назад, и несколько раз применил и остался доволен, счастлив и т.д. Что такое отражение? Это когда луч, падающий на поверхность, отбивается от этой поверхности на тот же самый угол. Угол, конечно же, между перпендикулятором к поверхности (нормаль) и самой поверхностью: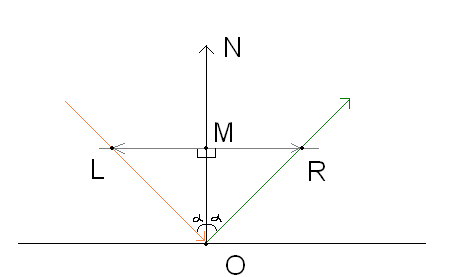

Что мы видим? Я вижу, что надо провести проекцию точки L в точку M, чтобы образовался прямоугольний треугольник (как же без него?). Потом можно будет, зная вектор проекции, узнать также вектор проекции с другой стороны, с точки R на точку M. Что мы знаем? Мы знаем вектор OL (падающий луч) и вектор ON (нормаль). Нужно узнать вектор OR (отраженный луч). Договоримся так, что все вектора имеют единичную длину, чтобы не морочить себе голову с вычислениями длин.
Для начала, вспомним, что OM - это прилежащий катет к гипотенузе OL, а это значит, что:
Вместо OM, OL, ON и пр, буду писать просто M, L, N и т.д.
Итак, мы узнали длину M, это важно, теперь надо узнать, где именно этот M будет, какие у него координаты, это сделать очень просто, а еще, если вспомнить, что , это скалярное произведение векторов:
Половина дела сделана, мы узнали, где будет точка M, а теперь бы неплохо узнать вектор ML, это делается просто вычитанием: из точки L вычитаем точку M:
Теперь же, чтобы найти точку R, надо полученный вектор ML вычесть из точки M, чтобы прийти в точку R:
Здесь просто этот самый ML зеркально отражается от точки M, получается. Подставляем вместо ML:
Зная, как вычисляется M, получаем:
Да это же элементарно, Ватсон!