Главная » Математика » Скалярное произведение векторов
В избранное

§ Докажем?

Для начала, надо опять рассмотреть какой-то треугольник. Тут все в треугольниках.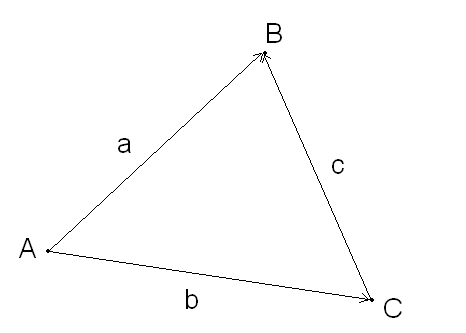

Нам известны 2 вектора, это вектор a и вектор b , и всё. Ну еще координаты известны у этих векторов, и именно вектора мы и будем рассматривать. Вот тут есть один важный момент:
\vec{c} = \vec{b} - \vec{a}
Теперь у нас есть и вектор \vec{c} . Теперь надо взять теорему косинусов:
c^2 = a^2 + b^2 - 2abcos(\alpha)
Сделаем так. Обозначим abcos(\alpha) в виде вот такого символа \langle A,B\rangle
(b-a)^2 = a^2 + b^2 - 2 \langle A,B\rangle
Как мы должны понимать, нужно найти длины a , b , c , а координаты заданы у нас в виде x,y , потому
a = (x_1,y_1)
b = (x_2,y_2)
c = b - a = (x_2-x_1,y_2-y_1)
Найдем длины каждого вектора
|a| = \sqrt{x_1^2+y_1^2}
|b| = \sqrt{x_2^2+y_2^2}
|b-a| = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2}
Подставляем значения в формулу теоремы косинусов
\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}^2 = \sqrt{x_1^2+y_1^2}^2 + \sqrt{x_2^2+y_2^2}^2 - 2 \langle A,B\rangle
Сразу ясно, что квадраты ликвидируют корни
(x_2-x_1)^2+(y_2-y_1)^2 = x_1^2+y_1^2 + x_2^2+y_2^2 - 2 \langle A,B\rangle
Раскрываем скобки и перенесем куда требуется
- 2 \langle A,B\rangle = (x_2^2-2x_1x_2+x_1^2)+(y_2^2-2y_1y_2+y_1^2) - x_1^2 - y_1^2 - x_2^2 - y_2^2
После того, как сократим, вот что останется
-2\langle A,B\rangle = -2x_1x_2-2y_1y_2
И вот что получается:
\langle A,B\rangle = x_1x_2+y_1y_2
Теперь по-другому сделаем, заменим символ скалярного произведения на его эквивалент, который ранее заменяли
abcos(\alpha) = x_1x_2+y_1y_2
Заметим, что a и b тут длины, поэтому
cos(\alpha) = \frac{x_1x_2+y_1y_2}{\sqrt{x_1^2+y_1^2}\sqrt{x_2^2+y_2^2}}
Какой можно сделать вывод? Очень простой - имея координаты векторов, мы можем рассчитать косинус, и по косинусу угол между векторами. Если вектора единичные, то есть их длины равны 1, то тогда еще проще получается
cos(\alpha) = x_1x_2+y_1y_2
Вычислить же угол вот так можно, через арккосинус
\alpha = arccos(x_1x_2+y_1y_2)
Спасибо, что все понятно. А точно ли все понятно? Этот вопрос остается открытым...
12 мая 2020, 14:25
© 2011-2025 Мочил слабый Мармок