§ Любопытный вопрос
Для задачи по дискретному преобразованию Фурье, которое я исследую, мне потребовалось узнать справедливость вычисления интеграла через последовательность сумм, или, проще говоря, проверить, можно ли найти интеграл таким образом и будет ли это справедливо.Что такое определенный интеграл? Это просто площадь функции от точки до точки .
Я хочу взять какую-то самую простую функцию и попробовать подсчитать по ней интеграл. Возьму функцию и подсчитаю для нее интеграл от 0 до :
§ Расчет площади по прямоугольникам
На иллюстрации зеленым обозначена площадь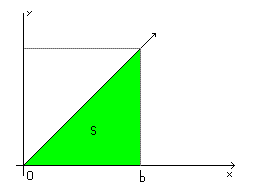
Ясное дело, что такую простую фигуру подсчитать можно и по формуле расчета площади прямоугольного треугольника , но я хочу показать, что можно пересчитать также и через последовательность кусочков:
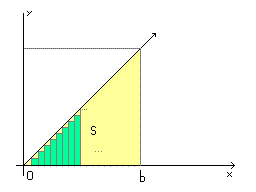
Разделим область от 0 до b на N прямоугольников. Высота прямоугольника будет равна , где . Ну или другими словами, пробегает от 0 до b по кускам. Соответственно n (номер прямоугольника) пробегает от 1 до N. Высота известна, а ширина прямоугольника будет равна . Теперь составлю формулу для расчета всех прямоугольников для функции:
Это общее представление для любой функции, но так как , то получается вот так
Абсолютно нетрудно заметить, что, собственно говоря, справа получается обыкновенная арифметическая прогрессия от 1 до N. Поскольку формулу для такой арифметической прогрессии я получил еще в 10 лет, то вот я сразу же ее привожу:
Впишу ее в предыдущую формулу
Теперь, когда уравнение для получения суммы было найдено, скажу сразу - чем больше будет N, тем выше точность вычисления, и ясное дело, что чем ниже N, то тем она ниже. Если взять N таким огромным, то одна из частей уравнения просто обнулится. Если же N будет стремиться к бесконечности, то и будет стремиться к . Это и есть лимиты.
А значит, можно считать, что метод вычисления через сумму прямоугольников совершенно верный. Естественно, можно считать интеграл чуть быстрее, используя либо метод трапеции, либо сплайнов, но в самом предельном своем случае, достаточно лишь метода прямоугольников.
У меня пока все, это все, что я хотел сказать по поводу вычисления интеграла от x. Что-то сложно выходит. Цель моя была только показать возможность и точность такого рода вычисления.