11:58
Точное текстурирование в 3D — Лисья нора
* Точка на параллепипеде
* Пересечение прямой и плоскости
* Жесткая линейная алгебра
* Программная реализация
некоторые азы аналитической геометрии. Ибо без этого никак просто и никуда, однако, она не такая и сложная, если
подумать.
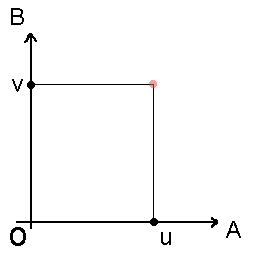
Рисунок 1. Точка в 2-х мерном пространстве
Вот возьмем очень простой пример, чтобы положить точку в 2-х мерном пространстве, нам потребуется отсчитать некоторую длину по оси , зафиксировать там точку, и отсчитать некоторую длину по оси . Точка будет как раз там. С математической точки зрения это будет выглядеть так:
То есть, если мы возьмем, например , , то получится вот что:
А теперь рассмотрим другой случай. С параллелепипедом.
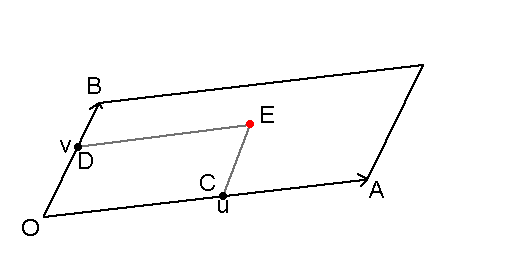
Рисунок 2. Точка на параллелепипеде
На этом рисунке видно, что сначала мы откладываем на прямой некоторый отрезок длиной , и на прямой отрезок длиной , после чего делаем их пересечение, но на самом деле, это сложение. Вот так получаем точку на отрезке
И также делается для отрезка для получения точки :
Как видно, я сразу сделал все в трехмерных координатах, чтобы проиллюстрировать, что не имеет значения размерность. Но, чтобы получить точку , или, точнее сказать, вектор , необходимо сначала проложить вектор , и к нему добавить вектор (или наоборот, не имеет значения). Соответственно, базисом будет точка .
В векторной форме будет вот так (приблизительно говоря)
Итог. Таким образом, мы параметрически задали плоскость в пространстве. То есть, чтобы описать любую плоскость в пространстве, для этого нам потребуется пара , и 3 точки, а точнее даже говоря, 2 вектора.
параметры , которые и будут координатами текстуры. Условимся в том, что и . То есть позиция текстуры не будет выпадать за пределы от 0 до 1. Что и правильно на первых порах. Так-то она часто как раз превышает эти пределы, чтобы текстуру "размножить" на один треугольник можно было.
Каким образом найти пересечение прямой и плоскости, которые заданы параметрически? Оба заданы? Нужно их приравнять друг к другу. То есть, чтобы сделать, чтобы точка лежала на плоскости, надо, что точка эта была равна уравнению этой плоскости. Допустим, у нас есть параметрически заданная прямая . Мы приравняем каждый ее компонент к уравнению плоскости, заданную векторами и .
Теперь задача в том, чтобы найти . Точкой пересечения будет точка . Она пока не нужна, нам нужны только 2 параметра, которые будут пересекаться (если еще будут), могут и не пересечься, если линия лежит параллельно плоскости, в таком случае хоть какие взять параметры, они не сойдутся.
Для начала, я все-таки кое-что сокращу. А то писать уж очень много. Сделаю так:
Теперь я то большое уравнение запишу в другой форме, сокращенно и перенесу сразу, чтобы было на своих местах.
Если присмотреться, то можно заметить, что это система линейных алгебраических уравнений (СЛАУ) с тремя неизвестными. То есть, его можно решить методом Крамера запросто. Либо методом Гаусса, кому как удобнее. Я решаю их методом Крамера всегда. Решать я его не буду сейчас, это легко сделать самому. И не суть еще. Это лишь иллюстрация к дальнейшим формулам.
Сейчас я последовательно выведу формулу, по которой можно подсчитывать , зная лишь точку проекции , ну и координаты расположенной в пространстве плоскости (треугольника).
Рассмотрим уравнение проекции.
Мы знаем здесь , потому что задаем точку на экране и хотим вычислить параметры . Перезапишем иначе, я перенесу w, h в левую часть уравнения (и знак поменяю, где ):
Условимся, что:
Чтобы потом легче было считать. Теперь я сокращу также и другое:
И для y:
Здесь – это именно координаты проекции, т.е. координаты точки на экране. Домножу левую и правую половину на одно и то же выражение, чтобы получить следующее
Нужно поставить на место , чтобы найти u:
* Пересечение прямой и плоскости
* Жесткая линейная алгебра
* Программная реализация
§ Точка на параллепипеде
Это любимая тема, текстурирование. И сейчас про нее и будет идти разговор. Но для начала, надо вспомнитьнекоторые азы аналитической геометрии. Ибо без этого никак просто и никуда, однако, она не такая и сложная, если
подумать.

Рисунок 1. Точка в 2-х мерном пространстве
Вот возьмем очень простой пример, чтобы положить точку в 2-х мерном пространстве, нам потребуется отсчитать некоторую длину по оси , зафиксировать там точку, и отсчитать некоторую длину по оси . Точка будет как раз там. С математической точки зрения это будет выглядеть так:
То есть, если мы возьмем, например , , то получится вот что:
А теперь рассмотрим другой случай. С параллелепипедом.

Рисунок 2. Точка на параллелепипеде
На этом рисунке видно, что сначала мы откладываем на прямой некоторый отрезок длиной , и на прямой отрезок длиной , после чего делаем их пересечение, но на самом деле, это сложение. Вот так получаем точку на отрезке
И также делается для отрезка для получения точки :
Как видно, я сразу сделал все в трехмерных координатах, чтобы проиллюстрировать, что не имеет значения размерность. Но, чтобы получить точку , или, точнее сказать, вектор , необходимо сначала проложить вектор , и к нему добавить вектор (или наоборот, не имеет значения). Соответственно, базисом будет точка .
В векторной форме будет вот так (приблизительно говоря)
Итог. Таким образом, мы параметрически задали плоскость в пространстве. То есть, чтобы описать любую плоскость в пространстве, для этого нам потребуется пара , и 3 точки, а точнее даже говоря, 2 вектора.
§ Пересечение прямой и плоскости
Пришло время рассказать о том, как найти пересечение прямой и плоскости. Это важно, поскольку мы должны найтипараметры , которые и будут координатами текстуры. Условимся в том, что и . То есть позиция текстуры не будет выпадать за пределы от 0 до 1. Что и правильно на первых порах. Так-то она часто как раз превышает эти пределы, чтобы текстуру "размножить" на один треугольник можно было.
Каким образом найти пересечение прямой и плоскости, которые заданы параметрически? Оба заданы? Нужно их приравнять друг к другу. То есть, чтобы сделать, чтобы точка лежала на плоскости, надо, что точка эта была равна уравнению этой плоскости. Допустим, у нас есть параметрически заданная прямая . Мы приравняем каждый ее компонент к уравнению плоскости, заданную векторами и .
Теперь задача в том, чтобы найти . Точкой пересечения будет точка . Она пока не нужна, нам нужны только 2 параметра, которые будут пересекаться (если еще будут), могут и не пересечься, если линия лежит параллельно плоскости, в таком случае хоть какие взять параметры, они не сойдутся.
Для начала, я все-таки кое-что сокращу. А то писать уж очень много. Сделаю так:
Теперь я то большое уравнение запишу в другой форме, сокращенно и перенесу сразу, чтобы было на своих местах.
Если присмотреться, то можно заметить, что это система линейных алгебраических уравнений (СЛАУ) с тремя неизвестными. То есть, его можно решить методом Крамера запросто. Либо методом Гаусса, кому как удобнее. Я решаю их методом Крамера всегда. Решать я его не буду сейчас, это легко сделать самому. И не суть еще. Это лишь иллюстрация к дальнейшим формулам.
§ Жесткая линейная алгебра
Сейчас пойдут формулы. И много. Очень много формул. Поэтому, можно не читать этот раздел. Можно сразу взять какой-нибудь готовый результат, например, нарисовать что-то на OpenGL, не заморачиваясь с формулами.Сейчас я последовательно выведу формулу, по которой можно подсчитывать , зная лишь точку проекции , ну и координаты расположенной в пространстве плоскости (треугольника).
Рассмотрим уравнение проекции.
Мы знаем здесь , потому что задаем точку на экране и хотим вычислить параметры . Перезапишем иначе, я перенесу w, h в левую часть уравнения (и знак поменяю, где ):
Условимся, что:
Чтобы потом легче было считать. Теперь я сокращу также и другое:
ABx = B.x – A.x, ACx = C.x – A.x ABy = B.y – A.y, ACy = C.y – A.y ABz = B.z – A.z, ACz = C.y – A.zИ это тоже ради того, чтобы сократить и так гору вычислений в будущем. Вспомним параметрически заданное уравнение плоскости:
x = Ax + u*ABx + v*ACx y = Ay + u*ABy + v*ACy z = Az + u*ABz + v*ACzТеперь эти я поставлю в уравнение проекции для x:
И для y:
Здесь – это именно координаты проекции, т.е. координаты точки на экране. Домножу левую и правую половину на одно и то же выражение, чтобы получить следующее
x(Az + u*ABz + v*ACz) = fov(Ax + u*ABx + v*ACx) y(Az + u*ABz + v*ACz) = fov(Ay + u*ABy + v*ACy)Раскрываем скобки
x*Az + u*x*ABz + v*x*ACz = fov*Ax + u*fov*ABx + v*fov*ACx y*Az + u*y*ABz + v*y*ACz = fov*Ay + u*fov*ABy + v*fov*ACyПриведем подобные
u*x*ABz – u*fov*ABx + v*x*ACz – v*fov*ACx = fov*Ax – x*Az u*y*ABz – u*fov*ABy + v*y*ACz – v*fov*ACy = fov*Ay – y*AzСгруппируем:
u(x*ABz – fov*ABx) + v(x*ACz – fov*ACx) = (fov*Ax – x*Az) u(y*ABz – fov*ABy) + v(y*ACz – fov*ACy) = (fov*Ay – y*Az)Как теперь видим, можно найти суть. Мы видим СЛАУ, который решается методом Крамера. То есть тут всего лишь 2 неизвестных, остальное все вычислимо. Теперь надо вспомнить метод Крамера и перемножить коэффициенты между собой особым (крест-накрест), образом
D = (x*ABz – fov*ABx)*(y*ACz – fov*ACy) –
(x*ACz – fov*ACx)*(y*ABz – fov*ABy)Это и будет детерминант. Он потребуется, чтобы вычислить u, v. Выносим все за скобки и начинаем пересчитывать между собой, сокращая все, что нужно:+x*y*ABz*ACz – x*fov*ABz*ACy – y*fov*ABx*ACz + fov2*ABx*ACy -x*y*ABz*ACz + x*fov*ACz*ABy + y*fov*ACx*ABz – fov2*ABy*ACxИ D будет равно:
x*fov* (ABy*ACz – ABz*ACy) + y*fov* (ABz*ACx – ABx*ACz) + fov2*(ABx*ACy – ABy*ACx)Все! Детерминант подсчитан. Начинаем считать u. Подставим необходимые коэффициенты по методу крамера.
Нужно поставить на место , чтобы найти u:
u(fov*Ax – x*Az) + v(x*ACz – fov*ACx) u(fov*Ay – y*Az) + v(y*ACz – fov*ACy)Перемножим крест-накрест :
(fov*Ax – x*Az)*(y*ACz – fov*ACy) – (x*ACz – fov*ACx)*(fov*Ay – y*Az) = fov*y*Ax*ACz – x*y*ACz*Az – fov2*Ax*ACy + fov*x*Az*ACy -fov*x*Ay*ACz + x*y*ACz*Az + fov2*Ay*ACx – fov*y*Az*ACxВ итоге выходит:
u' = x*fov* (Az*ACy – Ay*ACz) + y*fov* (Ax*ACz – Az*ACx) + fov2*(Ay*ACx – Ax*ACy)Аналогичным образом, делается и для v:
u(x*ABz – fov*ABx) + v(fov*Ax – x*Az) u(y*ABz – fov*ABy) + v(fov*Ay – y*Az)Перемножение крест-накрест:
(x*ABz – fov*ABx)*(fov*Ay – y*Az) – (fov*Ax – x*Az)*(y*ABz – fov*ABy) = (x*ABz*fov*Ay - x*ABz*y*Az - fov*ABx*fov*Ay + fov*ABx*y*Az) - (fov*Ax*y*ABz - fov*Ax*fov*ABy - x*Az*y*ABz + x*Az*fov*ABy) = x*fov*Ay*ABz - x*y*ABz*Az - fov2*Ay*ABx + fov*y*Az*ABx -y*fov*Ax*ABz + x*y*ABz*Az + fov2*Ax*ABy - fov*x*Az*AByПриведя подобные, получаем:
v' = x*fov* (Ay*ABz - Az*ABy) + y*fov* (Az*ABx - Ax*ABz) + fov2*(Ax*ABy - Ay*ABx)Все, теперь, чтобы получить и , надо поделить их на дискриминант:
§ Программа на С
В заключение разговора, я приведу программу на С, чтобы потом много не искать, а сразу брать готовые результаты отсюда.// Сначала, получаем разности float ABx = b.x - a.x, ACx = c.x - a.x, ABy = b.y - a.y, ACy = c.y - a.y, ABz = b.z - a.z, ACz = c.z - a.z; // Рассчитываем коэффициенты float A1 = fov*(a.z*ACy - a.y*ACz), A2 = fov*(a.x*ACz - a.z*ACx), A3 = fov2*(a.y*ACx - a.x*ACy), // --- B1 = fov*(a.y*ABz - a.z*ABy), B2 = fov*(a.z*ABx - a.x*ABz), B3 = fov2*(a.x*ABy - a.y*ABx), // --- C1 = fov*(ABy*ACz - ABz*ACy), C2 = fov*(ABz*ACx - ABx*ACz), C3 = fov2*(ABx*ACy - ABy*ACx); float D = x*C1 + y*C2 + C3; float u = x*A1 + y*A2 + A3; float v = x*A1 + y*A2 + A3; if (D != 0) { u /= D; v /= D; } else { u = v = 0; }