§ Что требуется определить

Задана прямая AB и точка C. Необходимо рассчитать кратчайшее расстояние от точки до прямой. И еще узнать с какой стороны от этой прямо лежит данная точка.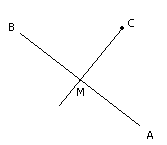

На рисунке изображена прямая AB и точка C, из которой опущена проекция MC. То есть, другими словами, треугольники AMC и BMC - прямоугольные. Первая задача в том, чтобы найти вектор MC, который был бы перпендикулярен AB. Для этого придется воспользоваться формулой поворота, и повернуть вектор AB на угол 90 градусов против часовой стрелки (влево).
Поворачиваем AB = {B.x-A.x, B.y-A.y}, зная что cos(90)=0, sin(90)=1:

x' = cos(90)*x - sin(90)*y = -y
y' = cos(90)*y + sin(90)*x = x

Получаем прямую CM = {A.y-B.y, B.x-A.x}. На самом деле вектор CM не получится так просто, дело в том, что длина полученного вектора будет равна вектору AB.

§ Точка пересечения

Найдем точки пересечения прямой AB и прямой MC в точке M. Они задаются параметрически:

x = A.x + u*(B.x - A.x)
y = A.y + u*(B.y - A.y)

Теперь надо выразить параметрически прямую MC. Она начинается с точки M, и ранее был вычислен вектор {A.y-B.y, B.x-A.x}, потому подставляются новые координаты:

x = C.x + v*(A.y - B.y)
y = C.y + v*(B.x - A.x)

Приравниваем между собой по x и y:

A.x + u*(B.x - A.x) = C.x + v*(A.y - B.y)
A.y + u*(B.y - A.y) = C.y + v*(B.x - A.x)

Переносим влево неизвестные и вправо, как обычно, известные:

u*(B.x - A.x) + v*(B.y - A.y) = C.x - A.x
u*(B.y - A.y) - v*(B.x - A.x) = C.y - A.y

Получилась типичная система линейных алгебраических уравнений (СЛАУ). Таким образом, нам осталось найти либо u, либо v, чтобы найти точку M и рассчитать расстояние до нее. Чтобы это сделать, необходимо рассчитать значение v по формуле Крамера. Я сразу же подсчитаю, чтобы опустить лишние вычисления:

     AB.y*AC.x - AB.x*AC.y
v = -----------------------
     AB.x*AB.x + AB.y*AB.y

Как можно тут обнаружить, в качестве детерминанта тут получилось скалярное произведение вектора AB. Так что детерминант тут никогда не будет отрицательным числом, по причине того, что каждый компонент вектора (x, y) возводится в квадрат.

§ На чьей стороне точка

Если полученный v больше 0, то тогда можно считать, что точка находится справа от вектора AB, поскольку прямая CM идет влево, то значит, при v > 0 прямая находится с левой стороны от точки, а следовательно, точка находится справа. Так же, если v < 0, точка находится слева от прямой, ну и если v = 0, то вообще на самой прямой.
Для того, чтобы определить сторону, на которой находится точка по отношению к прямой AB, необязательно рассчитывать детерминант. Он всегда будет положительным и ни на что влиять не будет. Поэтому достаточно лишь рассчитать вот эту формулу:

AB.y*AC.x - AB.x*AC.y

И по ее знаку определить, где лежит точка. Практическое применение этого метода состоит в том, что таким образом вырезаются невидимые грани при рендеринге треугольника. Если точка C треугольника лежит правее прямой AB, то тогда он отображается - иначе нет. Это экономит некоторое процессорное время на отрисовку - таким образом не прорисовываются некоторые лишние треугольники, которые лежат "задом" к наблюдателю.

§ Расстояние до прямой

Зная точку M и начальную точку C (которую надо найти), не составляет труда вычислить расстояние. Итак, надо рассчитать расстояние через теорему Пифагора. Сделаю подстановку:

AB.x = a,
AB.y = b,
AC.x = x - x0
AC.y = y - y0

А так вычисляется дистанция:

dist = sqrt((M.x - C.x)2 + (M.y - C.y)2)

Здесь получается так:

M.x - C.x = (C.x - v*b) - C.x = -v*b
M.y - C.y = (C.y + v*a) - C.y =  v*a

Ранее v был известен и вычисляется так
Вычисляем дистанцию по теореме Пифагора:
Теперь выполним подстановку v:
Поскольку sqrt(a) / a = 1 / sqrt(a), делаем так:
Таким образом, можно вычислить расстояние от точки до прямой:

     AB.y*AC.x - AB.x*AC.y
d = =========================
     SQRT( AB.x2 + AB.y2 )

Собственно, что и требовалось доказать.

§ Программа на Quick Basic

1SCREEN 13
2
3A = 1.1
4
5Ax = 160
6Ay = 100
7Bx = Ax + SIN(A) * 50
8By = Ay + COS(A) * 50
9
10ABx = Bx - Ax
11ABy = By - Ay
12
13FOR y = 0 TO 200
14FOR x = 0 TO 320
15
16  ACx = x - Ax
17  ACy = y - Ay
18
19  v = ABy * ACx - ABx * ACy
20  d = SQR(ABx ^ 2 + ABy ^ 2)
21
22  cl = 0
23  IF v > 0 THEN cl = v / d
24
25  PSET (x, 200 - y), cl
26
27NEXT
28NEXT