§ Графически-аналитически

На самом деле, тема очень простая. Необходимо рассчитать, где и каким образом пересекутся две прямые, с заданными векторами направления. Представим, что существует вектор AB и вектор CD. Необходимо найти точку пересечения M.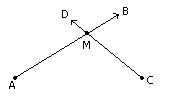

§ Задание линии параметрически

Задаем обе линии параметрическим методом.
Первая линия:
Вторая линия:

§ Решение уравнения

Потом приравниваем уравнения. Как можно заметить, существует некоторая общая точка (x,y), которая должна совпасть, когда у нас будет необходимый u, v. Приравниваем их:
Теперь переносим все неизвестные влево, а известные - вправо:
Заменим:
И вот что получилось:

§ Нахождение u, v, x, y

Как можно заметить, на самом деле это получилось обычное линейное уравнение, которое легко решается методом Крамера. Первым делом найдем определитель:
Если определитель равен 0, это означает только то, что линии параллельны и не имеют точек соприкосновения. Если же нет, то рассчитаем u. Для этого столбец справа, где AC, надо подставить в столбец слева, где AB и рассчитать определитель. После чего поделить на D.
Значит, что u будет равен вот этому выражению:
А также бывает полезно рассчитать v:
Зная легко рассчитать :
Или:
Вот и всё. Точно так же получается и с v - разницы нет, они все равно пересекаются. Интересный факт - если v лежит в диапазоне от 0 до 1, то точка лежит на отрезке CD, точно та же как и u=[0,1] лежит на отрезке AB.

§ Реализация на QB

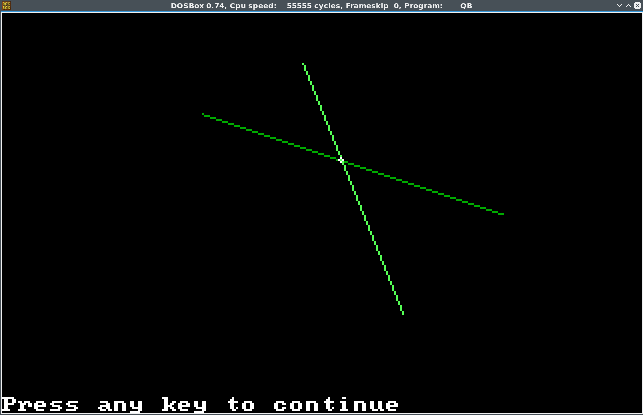
1SCREEN 13
2
3Ax = 100: Ay = 50: Bx = 250: By = 100
4Cx = 150: Cy = 25: Dx = 200: Dy = 150
5
6' ----------
7LINE (Ax, Ay)-(Bx, By), 2
8LINE (Cx, Cy)-(Dx, Dy), 10
9
10' ----------
11ABx = Bx - Ax: ABy = By - Ay
12ACx = Cx - Ax: ACy = Cy - Ay
13CDx = Dx - Cx: CDy = Dy - Cy
14
15D = (ABy * CDx - ABx * CDy)
16u = (ACy * CDx - ACx * CDy) / D
17v = (ABy * ACx - ABx * ACy) / D
18
19x = Ax + u * ABx
20y = Ay + u * ABy
21
22' ------------------
23CIRCLE (x, y), 1, 15