§ Теория

Сегодня рассмотрю как найти преломленный луч. Преломление это когда луч проходит из плотности одной среды в другую не под тем же самым углом.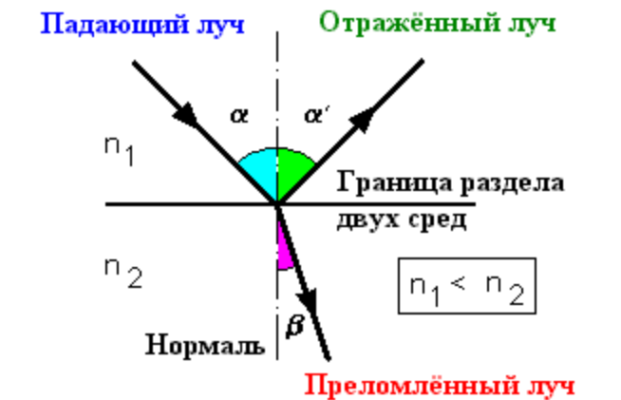

Рассмотрим картинку. Есть луч, который падает под углом по отношению к нормали. Луч может как отражаться, так и преломляться. Когда луч преломляется, часть света уходит далее, при этом преломленный луч отклоняется относительно нормали и приобретает угол .
Существует формула закона Снеллиуса:
Здесь n1 и n2 это коэффициент преломления среды. Угол падения и угол преломления . Например воздух имеет меньший коэффициент, чем вода.

• Для воды — 1.333
• Воздух — 1.000
• Алмаз — 2.419

Это просто список для примера. Еще стоит отметить, что помимо преломления существует и дисперсия, когда луч отклоняется тем больше, чем короче длина волны.

§ Вывод формулы

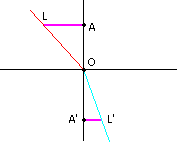
Задача найти вектор A'L'. Первое, что нужно найти это вектор OA. Это делается путем поиска через нормаль .
Теперь, чтобы найти вектор LA, потребуется вычесть A из L, то есть .
Теперь важный момент. Известно, что:

Поскольку полагаем, что OL и OL' равны 1, то переписываем так:
В итоге, получается, что найти A'L' можно так:
Но так можно найти только вектор A'L', но не OA'. Чтобы найти вектор OA', потребуется вычислить:
Итоговый вектор будет равен:

§ Второй вывод

Если OL равен 1 и нормаль тоже равна 1, то тогда , а также .
Поскольку знаем, чему равен
То можно узнать, чему равен , а именно
Из следующей формулы можно вывести, чему будет равен :
После преобразования
Теперь надо найти, чему будет равен :
Итоговый вектор будет равен:
Я бы не сказал, что это оптимальное решение, но что делать.
Причем, важный момент — это работать будет только если подкоренное выражение не отрицательное. Если оно отрицательное, то происходит полное внутреннее отражение.
Бывает такой случай, когда . Это значит, что произошло то, что произошло — при преломлении луч не преломился, а отразился.

§ Код

Этот код для того, чтобы проиллюстрировать отражение и преломление одновременно.

1float length(vec3 n) {
2    return sqrt(n.x*n.x + n.y*n.y + n.z*n.z);
3}
4
5// Нормализация вектора
6vec3 normalize(vec3 n) {
7
8    float l = length(n);
9          l = l ? 1/l : 1;
10
11    return {l*n.x, l*n.y, l*n.z};
12}
13
14// q - преломление n2/n1
15void render(vec3 L, vec3 N, float n1, float n2) {
16
17    float S = 90;
18    float q = n1 / n2;
19
20    N = normalize(N);
21    L = normalize(L);
22
23    // Нормаль и подложка под нее
24    app->line(160 - N.y*S, 100 - N.x*S, 160, 100, 0x606060); // Подложка
25    app->line(160 + N.y*S, 100 + N.x*S, 160, 100, 0x606060); // Подложка
26    app->line(160 + N.x*S, 100 - N.y*S, 160, 100, 0xc0c000); // +Нормаль
27    app->line(160 - N.x*S, 100 + N.y*S, 160, 100, 0x808000); // -Нормаль
28    app->line(160 + L.x*S, 100 - L.y*S, 160, 100, 0xf0f0f0); // Луч
29
30    // Вычисление <N,L>
31    float cosa = N.x*L.x + N.y*L.y + N.z*L.z;
32    float refl = 1 - q*q + q*q*cosa*cosa;
33    float cosb = refl >= 0 ? sqrt(refl) : 0;
34
35    vec3 K = {N.x*cosa - L.x,      N.y*cosa - L.y,      N.z*cosa - L.z};
36    vec3 R = {K.x      + N.x*cosa, K.y      + N.y*cosa, K.z      + N.z*cosa};
37    vec3 F = {K.x*q    - N.x*cosb, K.y*q    - N.y*cosb, K.z*q    - N.z*cosb};
38
39    // Построение луча отражения
40    app->line(160 + R.x*S, 100 - R.y*S, 160, 100, 0x00f000);
41
42    // Преломление. Если преломление превышает 90 градусов, то полное отражение
43    if (refl >= 0) app->line(160 + F.x*S, 100 - F.y*S, 160, 100, 0x80f080);
44}