§ Вступительное слово

Наверное, все знают, что видеокарты рисуют треугольники, закрашенные текстурами? Я думаю, что это достаточно общеизвестный факт. Сегодня я хочу максимально раскрыть тему того, как выполнять текстурирование треугольника, используя только лишь программные средства. Видеокарты делают так же, но делают они это, используя собственные вычислительные средства, однако принцип работы остается неизменным.
Этот материал предназначен для тех, кто знает курс школьной математики и геометрии. В этой статье я расскажу о том, как вывести уравнения, позволяющие получить точное текстурирование. Да, возможно, будет непросто, придется внимательно вчитываться и перечитывать, но в итоге, это должно быть понято.

§ Координаты в пространстве

Рассмотрим только декартову систему координат. Эта система основана на том факте, что все 3 измерения (и более) образованы векторами, которые образуют каждый с каждым прямоугольный угол в 90 градусов. Есть три направления - обычно их пишут как . Для начала, я пока расскажу о двух измерениях, поскольку их легче всего представить на экране монитора.

На рисунке видно, что точка А проецируется на оси x, y. Пока что здесь все должно быть предельно понятно. Но так может быть не всегда. Здесь углы осей равны 90 градусов и потому сделать проекцию точки не составляет никакого труда.
Все становится сложнее, когда оси направлены уже по-другому, например, как на картинке:

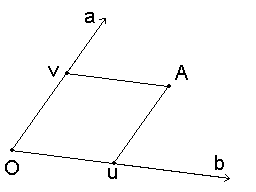
Есть ось и заданные векторами и . Здесь же - это проекция точки A по оси , а - проекция точки А по оси . Это лишь означает, что параллельна , а также параллельна . И всё. Почему я говорю обо всем этом? Дело в том, что это и есть тот самый треугольник, который нужно будет рисовать. Да, это похоже на обычный параллелограмм, но если его разделить на 2 части, то их него как раз и получится тот самый треугольник.
Еще раз замечу, что для понимания статьи требуются некоторые математические знания.
Теперь задача заключается вот в чем - сначала рассчитаем, точнее, найдем уравнение, по которому будет получаться точка A. Это уравнение очень простое. Поскольку есть координаты то не стоит никакого труда отложить по направлению вектора некий отрезок, а потом по направлению вектора тоже отложить отрезок, начало которого будет в конце предыдущего отрезка. Иначе говоря, с помощью сначала откладывается по одной оси расстояние, а потом откладывается по другой оси:
Тем самым, получая точку в пространстве, имея направляющие оси и не превышающие .

§ Расчет координат

Допустим, известны вектора и . Как видно, эти вектора - это именно направляющие оси параллелограмма, который рисуется с помощью этих вот двух векторов.
Теперь задача: зная точку в пространстве и два вектора, образующего параллелограмм, найти точки проекции , которые будут являться точками для текстуры, а точнее говоря, положениями точек в текстуре.
Для начала, я представлю уравнение в таком виде для двухмерного треугольника. Для трехмерного просто надо добавить еще одно измерение. Хотя там не все так и просто.
На самом деле легко увидеть, что получается обычное линейное уравнение с двумя неизвестными, которые легко решаются с помощью метода Крамера.
То есть, найдя определитель для уравнения, можно легко и просто получить
Получаем:
Найденные значения и будут точками текстуры на плоскости. Но это далеко не все. Здесь показан лишь линейный поиск без учета перспективной проекции, которая появляется при переходе к трехмерному пространству. А это уже другая тема для разговора.