§ Двухмерный треугольник

Как и обещал, создавать свои программы я буду, используя только средства Quick Basic 4.5, как самого любимого языка моего детства, собственно. Для наглядности, не переходя к 3Д проекции, я хочу рассказать о том, как можно разделить треугольник определенной рассекающей прямой. Ниже на рисунке приведу пример, что имею ввиду.

Здесь необходимо разбить треугольник таким образом, чтобы то что находилось за рассекающей прямой, не было видно. В движке, который использует заполнения треугольников определенным цветом или текстурой, необходимо создать либо один, либо два треугольника, чтобы отсечь лишнее. В проволочной графике достаточно лишь не рисовать определенные отрезки.

screen 13
line (0, 0)-(320, 200), 15, BF                ' БЕЛЫЙ ЭКРАН
data 50,25, 150,40, 74,120                    ' ТРИ ТОЧКИ ТРЕУГОЛЬНИКА
type P2: x as integer: y as integer: end type ' ОБЪЯВЛЕНИЕ ТИПОВ
dim t(0 to 2) AS P2                           ' ОБЪЯВЛЕНИЕ МАССИВА ТОЧЕК
for i = 0 to 2: read t(i).x, t(i).y: next     ' ЗАГРУЗКА ТОЧЕК В ПАМЯТЬ
for a = 0 to 2: b = (a + 1) mod 3: line (t(a).x, t(a).y) - (t(b).x, t(b).y), 0: next ' РИСОВАНИЕ ТРЕУГОЛЬНИКА

Я думал, что программа рисования треугольника будет более компактная, но ошибся. По итогу на экране появится следующая картинка.

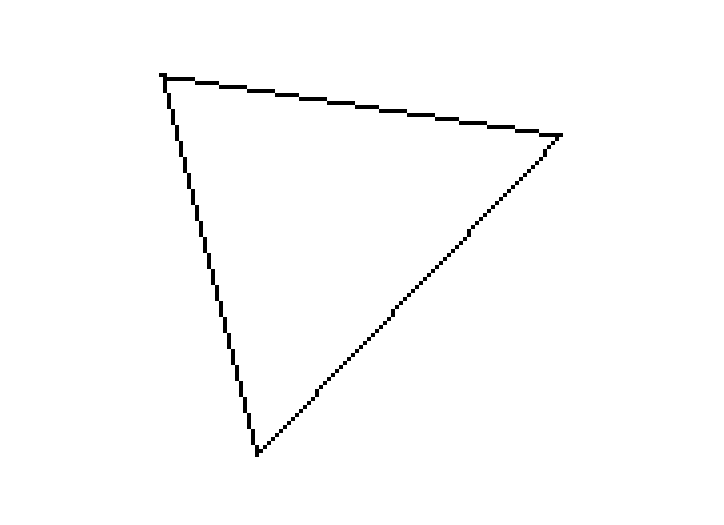
Задача в том, чтобы рассечь треугольник определенным образом так, чтобы часть его не рисовалась. И это как раз задача следующего параграфа.

§ Поиск точки пересечения

Итак, нам необходимо нарисовать каждую линию и проверить, не будет ли она пересекаться с рассекающей прямой. Существуют три варианта.

• Обе точки находятся в области перед рассекающей прямой. В этом случае, отрезок рисуется весь.
• Одна точка находится перед прямой, а вторая за ней. Тогда рисуется отрезок начиная с точки, которая видна, до точки пересечения с прямой.
• Обе точки не видны. Тогда и рисовать то нечего. Пропуск линии.

Но как нам понять, где и как будет проходить рассекающая линия? Для этого надо провести определенную прямую через две точки на прямой.
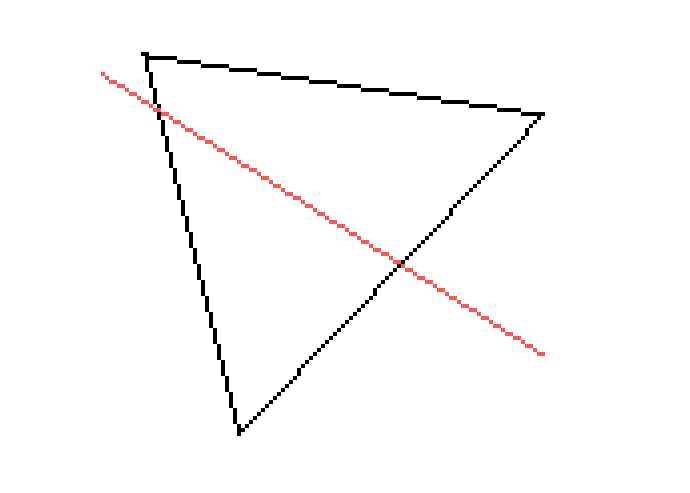
На рисунке выше, рядом с основным треугольником, нарисована рассекающая линия:

' РАССЕКАЮЩАЯ ПРЯМАЯ
x1 = 40: y1 = 30
x2 = 150: y2 = 100
line (x1, y1)-(x2, y2), 12

Теперь необходимо найти, как минимум, уравнение прямой. Ее удобнее всего задать параметрически:

x = x1 + u(x2 - x1)
y = y1 + u(y2 - y1)

Где x1,y1 это начало отрезка, x2,y2 точка конца отрезка и u - параметр, который меняется от 0 до 1 (начальная и конечная точка). На самом же деле, он может меняться от минус до плюс бесконечности.
Далее, при рисовании каждой из линии треугольника (и вообще любой линии, на самом деле), необходимо находить точки пересечения с этой прямой. Поскольку работа идёт в двухмерном пространстве, то найти точки пересечения прямых будет легко.
Возьмем любую из линии треугольника и найдем точку пересечения с рассекающей прямой. Параметрическое уравнение линии задается также как и нашей прямой.

x = A.x + t(B.x - A.x)
y = A.y + t(B.y - A.y)

Теперь, необходимо два этих уравнения приравнять между собой.

A.x + t(B.x - A.x) = x1 + u(x2 - x1)
A.y + t(B.y - A.y) = y1 + u(y2 - y1)

Перенесем неизвестные влево, а вправо известные.

u(x2 - x1) - t(B.x - A.x) = A.x - x1
u(y2 - y1) - t(B.y - A.y) = A.y - y1

Теперь необходимо найти одну из точек пересечения, а именно, ищем значение неизвестной t по методу Крамера — потому что она нам нужна.

D = (B.x - A.x)(y2 - y1) - (x2 - x1)(B.y - A.y)
T = (x2 - x1)(A.y - y1) - (A.x - x1)(y2 - y1)
t = t / D

И как это будет выглядеть на Бейсике.

x1 = 40: y1 = 30
x2 = 150: y2 = 100
dx = x2 - x1: dy = y2 - y1
line (x1, y1)-(x2, y2), 12

' РИСОВАНИЕ ТРЕУГОЛЬНИКА
for i = 0 to 2

  j = (i + 1) mod 3
  a = t(i): b = t(j)

  ' Для упрощения
  dxab = b.x - a.x
  dyab = b.y - a.y

  ' Вычисление пересечения
  D = dy*dxab - dx*dyab
  T = dx*(a.y - y1) - (a.x - x1)*dy
  t = T / D

  ' Линия
  line (a.x, a.y) - (b.x, b.y), 0

  ' Точка пересечения
  circle (a.x + t*dxab, a.y + t*dyab), 1, 2

next

Зеленые точки — это точки пересечения с рассекающей прямой. Теперь же рассмотрим варианты.

• Если то это значит, что точка пересечения лежит за пределами отрезка. То есть, иными словами, ничего делать не надо
• Если то конечная точка B пересекается с прямой ранее точки A, отрезок рисовать можно
• Если же то отрезок пересекается с одной из сторон и надо дорисовать до него
• Ну и если D = 0, то значит, отрезок вообще параллелен, он нигде не пересекается

На рисунке хорошо заметно что один из отрезков не пересекается с прямой, а остальные два — пересекаются.
Точки пересечения мы нашли, но ведь надо знать, с какой стороны лежит точка по отношению к рассекающему отрезку. Это очень важно для задачи, поскольку будем считать, что точки, которые лежат слева от вектора, который образует рассекающую, должны быть видны, а те что лежат справа — не видны.

§ Определение стороны

Задача в том, чтобы определить, с какой стороны лежит точка по отношению к некоторому вектору. Для того чтобы это определить, нам необходимо опустить прямую, которая была бы перпендикулярна вектору, что даст угол 90 градусов.
У нас есть вектор (x2-x1, y2-y1) с началом в точке (x1,y1). Не буду выводить формулу, но поворот на 90 градусов (влево) будет равен новому вектору (y2-y1,x1-x2), то есть из (dx,dy) получится (dy,-dx).

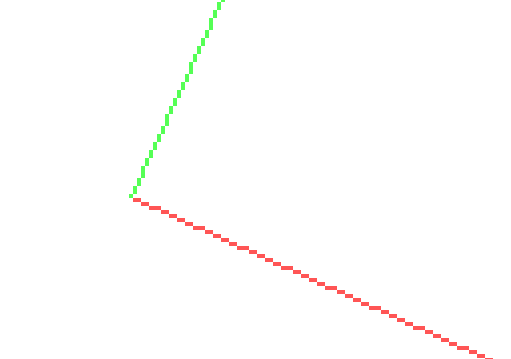
На рисунке показан исходный вектор (красный) и повернутый на 90 градусов влево зеленый вектор. Задача тривиальная. Из точки, по которой надо определить, где она лежит, надо опустить этот перпендикуляр и определить точку пересечения его, так же, задать параметрически. Единственное, чтобы результат был более корректным, вектор лучше развернуть в обратную сторону, то есть сделать не (dy,-dx), а (-dy,dx) — в таком случае перпендикуляр будет опускаться из точки к прямой, и если будет точка пересечения с ним, то параметр t будет больше 0. Если вектор пересечется в t меньше чем 0, то значит, точка находится с другой стороны.
Возьмем точку A с координатами (x,y) и отрезок (x1,y1)-(x2,y2). Составляем параметрическое уравнение перпендикулярной линии:

x = A.x - dy*t
y = A.y + dx*t

А также уже известное уравнение самой прямой:

x = x1 + dx*u
y = y1 + dy*u

Приравнивания, получаем систему линейных уравнений.

A.x - dy*t = x1 + dx*u
A.y + dx*t = y1 + dy*u

Необходимо найти t. Находится тем же самым методом, что и ранее.

A.x - x1 =  dy*t + dx*u
A.y - y1 = -dx*t + dy*u

Собственно, здесь детерминант матрицы будет dy*dy + dx*dx, что всегда является положительным числом, кстати говоря, и потому не повлияет на знак. И вообще для этой цели можно отбросить его. Остается найти знак t: dx*(A.y-y1) - dy*(A.x-x1).
Вычисляя эту функцию, можно точно узнать с какой стороны находится точка.

Там где синяя область — точка находится слева, там где зеленая — справа. Ниже программа, когда демонстрирует это.

' ПАРАМЕТРЫ ПРЯМОЙ
x1 = 40:  y1 = 30
x2 = 150: y2 = 100
dx = x2 - x1: dy = y2 - y1

for y = 0 to 200
for x = 0 to 320

  t = dx*(y-y1) - dy*(x-x1)
  if t > 0 then pset(x,y),2 else pset(x,y),1

next
next

§ Сборка кода воедино

Пришло время наконец, собрать все в одну кучу и выдать результат.
Итак, при рисовании одной линии, надо будет определять, какие точки находятся слева, а какие справа. Как выяснили, то точки, которые находятся слева от линии, будут иметь отрицательное значение, и наоборот.

sidea = dx*(a.y - y1) - dy*(a.x - x1)
sideb = dx*(b.y - y1) - dy*(b.x - x1)

Здесь, если sidea меньше 0, то будем считать, что точка A лежит в видимой области. Также, для точки B.
Соответственно, если точки обе находится слева, то рисовать такую линию всю.

if sidea < 0 and sideb < 0 then line (a.x, a.y) - (b.x, b.y), 0

В случае, если точки точки лежат слева и справа (либо A слева, B справа, либо наоборот, то условие будет таким).

if (sidea > 0 and sideb < 0) or (sidea < 0 and sideb > 0) then

Считаем точку пересечения.

dxab = b.x - a.x
dyab = b.y - a.y
D   = dy*dxab - dx*dyab
t   = sidea / D
cx  = a.x + t*dxab
cy  = a.y + t*dyab

Здесь C(x,y) это и есть точка пересечения, причем она идет со стороны точки A, следует отметить. Как видно, я заменил формулу dx*(a.y - y1) - dy*(a.x - x1) на sidea, так как она уже была ранее рассчитана.
Теперь же осталось узнать, с какой стороны рисуется отрезок. Если A лежит слева, то от этой точки до точки пересечения C, либо наоборот, от B к C.

' Либо точка A лежит слева
if sidea < 0 then line (a.x, a.y) - (cx, cy), 0

' Либо точка B лежит слева
if sideb < 0 then line (b.x, b.y) - (cx, cy), 0

§ Полный текст программы

Без этого никуда.

screen 13
line (0, 0)-(320, 200), 15, BF
data 50,25, 150,40, 74,120
type P2: x as integer: y as integer: end type
dim t(0 to 2) as P2
dim a as P2, b as P2
for i = 0 to 2: read t(i).x, t(i).y: next

' РАССЕКАЮЩАЯ ЛИНИЯ
x1 = 40:  y1 = 40
x2 = 180: y2 = 120
dx = x2 - x1: dy = y2 - y1
line (x1, y1)-(x2, y2), 2

' РИСОВАНИЕ ТРЕУГОЛЬНИКА
for i = 0 to 2

  j = (i + 1) mod 3
  a = t(i): b = t(j)

  ' Вычислить стороны
  sidea = dx*(a.y - y1) - dy*(a.x - x1)
  sideb = dx*(b.y - y1) - dy*(b.x - x1)

  ' Оба лежат слева
  if sidea < 0 and sideb < 0 then line (a.x, a.y) - (b.x, b.y), 0

  ' Одна из точек находится на пересечении
  if (sidea > 0 and sideb < 0) or (sidea < 0 and sideb > 0) then

    dxab = b.x - a.x
    dyab = b.y - a.y

    t = sidea / (dy*dxab - dx*dyab)

    cx = a.x + t*dxab
    cy = a.y + t*dyab

    ' Либо точка A лежит слева
    if sidea < 0 then line (a.x, a.y) - (cx, cy), 0

    ' Либо точка B лежит слева
    if sideb < 0 then line (b.x, b.y) - (cx, cy), 0

  end if

next

И результат выполнения

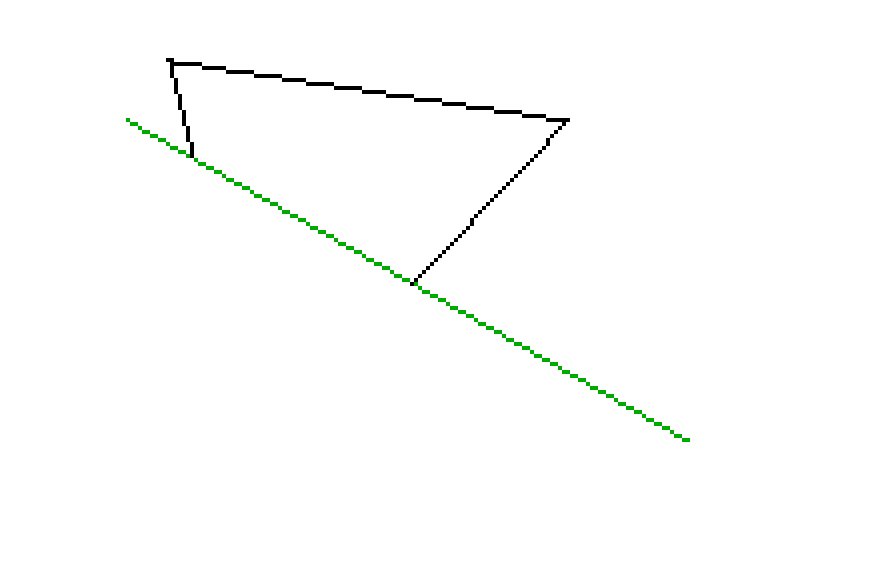
Но это еще не всё. С помощью данного метода можно также вычислять точки пересечения с другими объектами и делать более сложное отсечение невидимых линии.