Главная » Графика » Отражение луча от прямой

§ Постановка задачи

После того, как я объяснил, как найти точку пересечения прямой с другой прямой, мне интересно также разобрать тему, как сделать отражение такого луча от этой прямой.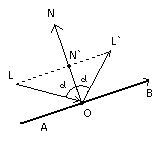

Рисунок 1
Здесь, на картинки, схематично изображен падающий луч LO на прямую AB. Луч пересекается с прямой в точке O и отражается из O в OL' (L со штрихом). Необходимо получить вектор OL' - отраженный луч.

§ Нормализация

Первым делом, перед решением этой задачи, необходимо найти нормаль и нормализовать вектор брошенного луча на прямую. Сначала нормализуем два вектора: AB и LO. Что такое нормализация? Это по сути, деление на такое число, при котором длина вектора будет равна 1, то есть, другими словами, надо сделать так, чтобы |AB| = 1 и |LO| = 1. Это сделать очень просто, первым делом надо рассчитать длину вектора и разделить этот вектор на эту длину. В итоге мы получим вектор длины 1.
Пример. Есть вектор AB={3,4}. Длина этого вектора находится по теореме Пифагора, которая гласит, что a2 + b2 = c2. В данном случае a - это компонента вектора x, b - y, c - это длина:
|AB| = \sqrt{x^2+y^2} = \sqrt{3^2 + 4^2} = \sqrt{25} = 5
Соответственно, если каждый компонент вектора AB разделить на 5, то получится вектор единичной длины. Проверим это:
AB=\{\frac{3}{5},\frac{4}{5}\}
|AB|=\sqrt{(\frac{3}{5})^2 + (\frac{4}{5})^2} = \sqrt{\frac{9}{25} + \frac{16}{25}} = \sqrt{1} = 1
Поэтому в общем виде формула нормализации для вектора будет выглядеть примерно так:
AB' = \frac{AB}{\sqrt{(B_x-A_x)^2+(B_y-A_y)^2}}

§ Нормаль

Теперь же, после того как вектора стали единичной длины, с ними уже можно работать нормально. Это необходимо для того, чтобы далее применять некоторые важные формулы, а именно скалярное произведение векторов для получения косинуса угла между ними.
Как можно догадаться, нормаль - это перпендикулярный вектор единичной длины к прямой или плоскости. Для того, чтобы его получить, необходимо повернуть исходный вектор либо на 90 градусов влево, либо на 90 градусов вправо. Я буду поворачивать его на 90 градусов влево.
Существует формула для поворота точки вокруг координатной оси на угол α:
x' = x cos \alpha - y sin \alpha
y' = y cos \alpha + x sin \alpha
По этой формуле, чтобы повернуть точку вокруг оси влево на 90 градусов, надо поставить α=90, отчего cos(90)=0, sin(90)=1:
x' = x*0 - y*1 = -y
y' = y*0 + x*1 = x
Следовательно, нормаль будет такой N={-AB.y, AB.x}. Собственно, с этим всё. Переходим к следующему вопросу.

§ Проекция луча на нормаль

Сначала начнем с определения, что такое косинус: это отношение прилежащего катета к гипотенузе в прямоугольном треугольнике. Поскольку на словах совершенно ничего не ясно, нарисую это: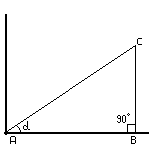

Рисунок 2
На этой картинке изображен прямоугольник треугольник ABC. Так вот, косинус угла α равен \frac{|AB|}{|AC|} - то есть, необходимо поделить длину AB на длину AC и получить косинус.
Однако это лишь половина дела. На самом деле тот же самый косинус можно получить, используя так называемое скалярное произведение векторов (при условии, что оба вектора AB и AC - нормализованы!), то есть так:
cos(\alpha) = AB_xAC_x + AB_yAC_y
Хорошо, допустим, что косинус угла α между нормалью ON и лучом OL мы получили успешно. Замечу, кстати, что вектора OL и ON должны быть направлены в одну сторону, а не в разную - надо, чтобы косинус получится положительным числом, то есть, чтобы угол α был меньше 90! Если же он получился отрицательным числом, это значит, что луч падает на поверхность или прямую с другой стороны. Это уже другой случай - а именно, преломление или вообще такой луч нельзя считать отраженным.
На рисунке 1 есть отрезок ON' - вот его как раз нам и надо получить, чтобы рассчитать отраженный луч. Как это сделать? Если посмотреть на рисунок 2, то этому отрезку ON' будет соответствовать вектор AB, а вектору OL будет соответствовать вектор AC. Поскольку OL нормализован, то его длина будет равна 1. Как же теперь получить AB (или ON' )?
cos(\alpha) = \frac{|AB|}{|AC|} = \frac{|ON'|}{|OL|}
Отсюда видно, что длина ON' легко выводится из длины вектора OL .
|ON'| = |OL| cos(\alpha) = cos(\alpha)
Стоит заметить, что раз вектор OL нормализован, то в таком случае |OL|=1 и |ON'| будет равен косинусу угла между вектором L и вектором нормали N (которая тоже равна 1).
Длину вектора мы знаем - но не знаем его направления. Чтобы это сделать, необходимо домножить вектор нормали (а он единичной длины) на полученный косинус:
N'.x = N.x * cos(α)
N'.y = N.y * cos(α)
Либо это записывается в общем виде так:
N' = \vec{N}\langle \vec{N},\vec{L}\rangle

§ Вычисление отражения

Теперь же - самое интересное. Необходимо теперь найти вектор OL' . Для этого нам потребуется узнать вектор LN' . Это делается очень просто: всего лишь надо вычесть из вектора ON' вектор OL и получим вектор LN' :
LN.x = N'.x - L.x
LN.y = N'.y - L.y
Теперь же полученный LN добавим к ON' и получится вектор OL' !
L'.x = N.x + LN.x = N.x + (N.x - L.x) = 2*N'.x - L.x
L'.y = N.y + LN.y = N.y + (N.y - L.y) = 2*N'.y - L.y
Помним, что:
N'.x = cos(α)*N.x
N'.y = cos(α)*N.y
А также еще то, что cos(α) на самом деле скалярное произведение векторов N и L.
L'.x = 2*N.x*cos(α) - L.x
L'.y = 2*N.y*cos(α) - L.y
Вот такая вот загогулина получается!
В общем виде эта формула вот так выглядит, она универсальна и подходит не только для 2D, но и для 3D:
L' = 2\vec{N}\langle \vec{N},\vec{L}\rangle - \vec{L}
Я уже ранее писал про зеркальное отражение. Фактически это просто повтор материала из той статьи.

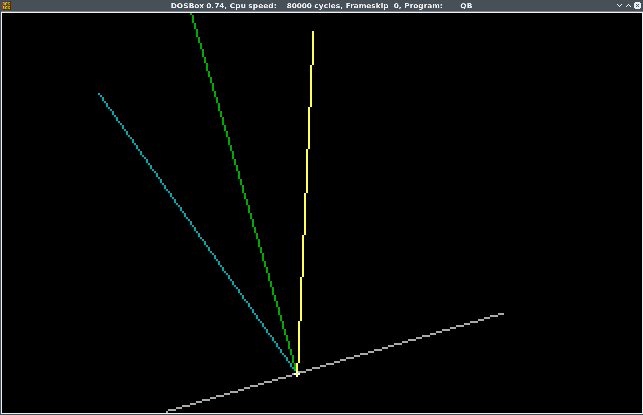
§ Программа на QB

Я написал интерактивную программу на QB, которая позволяет посмотреть, что происходит с отражением луча:
1SCREEN 13
2
3A = 0
4
5DO
6CLS
7
8' Подложка
9Ax = 50 + COS(A) * 25: Ay = 20 - SIN(A) * 30
10Bx = 250: By = 50
11
12' Луч
13Cx = 25 + SIN(A / 2) * 50: Cy = 130 + COS(A) * 50
14Dx = 150: Dy = 15
15
16' Получение нормали
17Nx = -(By - Ay)
18Ny = (Bx - Ax)
19
20' Вычисление точки пересечения луча и подложки
21ABx = Bx - Ax: ABy = By - Ay
22ACx = Cx - Ax: ACy = Cy - Ay
23CDx = Dx - Cx: CDy = Dy - Cy
24
25D = ABy * CDx - ABx * CDy
26v = (ABx * ACy - ABy * ACx) / D
27x = Cx + v * CDx
28y = Cy + v * CDy
29
30' Рисование линии нормали, подложки и луча
31LINE (Ax, 200 - Ay)-(Bx, 200 - By), 7
32LINE (Cx, 200 - Cy)-(x, 200 - y), 3
33LINE (x, 200 - y)-(x + Nx, 200 - (y + Ny)), 2
34
35' Вектор L
36Lx = Cx - x
37Ly = Cy - y
38
39' Нормализация вектора L, N
40Ln = SQR(Lx ^ 2 + Ly ^ 2)
41Nn = SQR(Nx ^ 2 + Ny ^ 2)
42
43Lx = Lx / Ln: Nx = Nx / Nn
44Ly = Ly / Ln: Ny = Ny / Nn
45
46' Скалярное произведение
47NL = Lx * Nx + Ly * Ny
48
49' Вычисление отражения
50Rx = 2 * Nx * NL - Lx
51Ry = 2 * Ny * NL - Ly
52
53' Восстановление длины вектора L
54Rx = Rx * Ln
55Ry = Ry * Ln
56
57' Отраженный вектор (желтый)
58LINE (x, 200 - y)-(x + Rx, 200 - (y + Ry)), 14
59
60' Установить точку пересечения
61CIRCLE (x, 200 - y), 1, 15
62
63' Движение
64A = A + .1
65SLEEP 1
66LOOP UNTIL 0
Номера

19 мар, 2021
© 2007-2024 Мышь кушает на дому